- #1
Shirish
- 244
- 32
I'm studying Core Principles of Special and General Relativity by Luscombe. In the section on Bondi's ##k##-factor, it says:
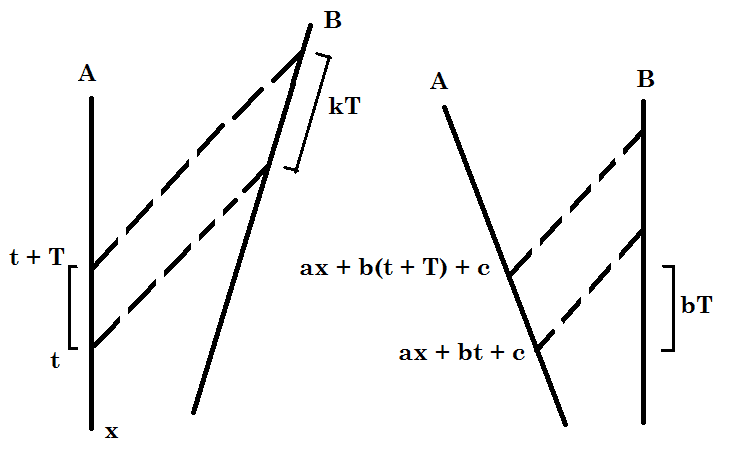
I want to clarify if my derivation of the above claim is correct. The image on the left is what's included in the text and referred to by the above paragraph. I made the image on the right to understand what's going on with linear transformation of worldlines.
Let ##E_S## and ##E'_S## be the events corresponding to ##A## sending the two light signals, and let ##E_R## and ##E'_R## be those corresponding to ##B## receiving them. The claim is that if the time separation between ##E_S## and ##E'_S## is ##T## in ##A##'s frame, then the time separation between ##E_R## and ##E'_R## is ##kT## in ##B##'s frame.
Following the reasoning given in the bold line of the above paragraph, suppose I switch from ##A##'s frame to ##B##'s frame. Then the worldline of ##A## will undergo some linear transformation ==> I can assume that the time coordinate of ##E_S## will become ##ax+bt+c## and the time coordinate of ##E'_S## will be ##ax+b(t+T)+c##.
The time separation between ##E_S## and ##E'_S## will then be ##bT## in ##B##'s frame. Finally, from this we can get the time separation between ##E_R## and ##E'_R## in ##B## frame as being proportional to ##bT##, say ##r(bT)##, using simple geometry. The overall effect is that separation b/w ##E_R## and ##E'_R## in ##B##'s frame is proportional to that between ##E_S## and ##E'_S## in ##A##'s frame, with ##k=rb##.
Does that seem correct? Or is there a flaw in the derivation?
Let inertial observers ##A## and ##B## in relative motion carry identical clocks. ##A## sends two flashes of light to ##B##, a time ##T## apart. What time separation does ##B## measure? ... We know that worldlines of free particles are straight in IRFs, and that spacetime coordinates in different IRFs are related by a linear mapping. The time difference measured in B must therefore be proportional to ##T##, call it ##kT##.
I want to clarify if my derivation of the above claim is correct. The image on the left is what's included in the text and referred to by the above paragraph. I made the image on the right to understand what's going on with linear transformation of worldlines.
Let ##E_S## and ##E'_S## be the events corresponding to ##A## sending the two light signals, and let ##E_R## and ##E'_R## be those corresponding to ##B## receiving them. The claim is that if the time separation between ##E_S## and ##E'_S## is ##T## in ##A##'s frame, then the time separation between ##E_R## and ##E'_R## is ##kT## in ##B##'s frame.
Following the reasoning given in the bold line of the above paragraph, suppose I switch from ##A##'s frame to ##B##'s frame. Then the worldline of ##A## will undergo some linear transformation ==> I can assume that the time coordinate of ##E_S## will become ##ax+bt+c## and the time coordinate of ##E'_S## will be ##ax+b(t+T)+c##.
The time separation between ##E_S## and ##E'_S## will then be ##bT## in ##B##'s frame. Finally, from this we can get the time separation between ##E_R## and ##E'_R## in ##B## frame as being proportional to ##bT##, say ##r(bT)##, using simple geometry. The overall effect is that separation b/w ##E_R## and ##E'_R## in ##B##'s frame is proportional to that between ##E_S## and ##E'_S## in ##A##'s frame, with ##k=rb##.
Does that seem correct? Or is there a flaw in the derivation?