- #1
g.lemaitre
- 267
- 2
Homework Statement
What am I supposed to do with the 3 over 2 in the parentheses? It can be divide and it can be take the factorial. So what do I do with it?
g.lemaitre said:Homework Statement
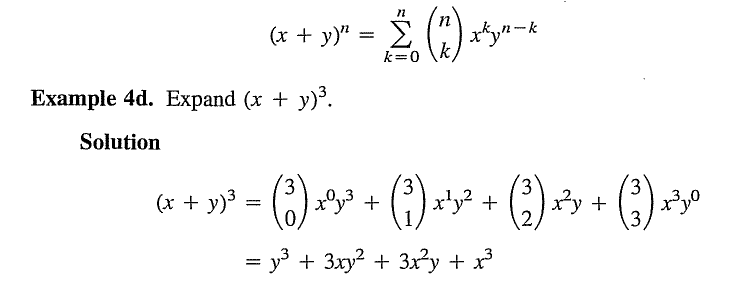
What am I supposed to do with the 3 over 2 in the parentheses? It can be divide and it can be take the factorial. So what do I do with it?
g.lemaitre said:Hi Infinitum! Call me Georges.
Does that mean you take 3!/2!? That work for the 3rd and 4th term but not for the second term and for the first term I think it's undefined.
The binary coefficient, [itex]\displaystyle \binom nk[/itex] is defined as follows.g.lemaitre said:Homework Statement
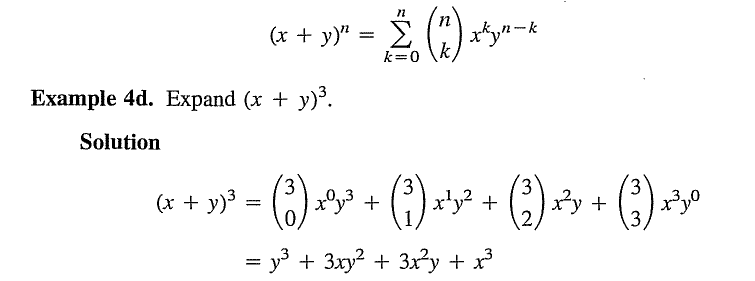
What am I supposed to do with the 3 over 2 in the parentheses? It can be divide and it can be take the factorial. So what do I do with it?
g.lemaitre said:Man, infinitum, you're such a big number it takes me like forever just to count you.
I understand the binomial coefficient and can get the right answer for terms 2 3 and 4 but I'm still having trouble with the first term.
if
[tex]\binom{n}{r} = \frac{n!}{r!(n-r)!}[/tex]
then
[tex]\binom{3}{0} = \frac{3!}{0!(3-0)!} = \frac{6}{0}[/tex]
The Binomial Theorem is a mathematical formula that allows us to expand binomials (expressions with two terms) raised to a positive integer power. It is commonly written as (a + b)^n and allows us to easily find the coefficients of each term in the expanded form.
The number 3/2 in parentheses is known as the power or exponent of the binomial. It represents the number of times the binomial is multiplied by itself in the expanded form. In other words, (a + b)^3/2 means that the binomial is multiplied by itself 3/2 times.
To solve problems involving the Binomial Theorem, you first need to identify the values of a, b, and n. Then, use the Binomial Theorem formula to expand the binomial and simplify the resulting expression. Finally, substitute in the given values to find the final answer.
No, the Binomial Theorem can only be applied to binomials with positive integer exponents. If the exponent is negative, the binomial should be rewritten with a positive exponent before applying the Binomial Theorem.
One tip for understanding the Binomial Theorem is to break down the expansion into smaller parts. For example, if the power is 5, you can first expand (a + b)^2, then (a + b)^3, and so on until you reach (a + b)^5. Also, remember that the coefficients of each term can be found using Pascal's Triangle.