- #1
kal854
- 13
- 0
Problem statement:
Two 3/4-in.-diameter nylon rods are spliced together by gluing a 2-in. section of plastic pipe over the rod ends, as shown in the figure. If a tensile force of P = 500 lb is applied to the spliced nylon rod, what is the average shear stress in the glue going between the pipe and rods?
Figure:
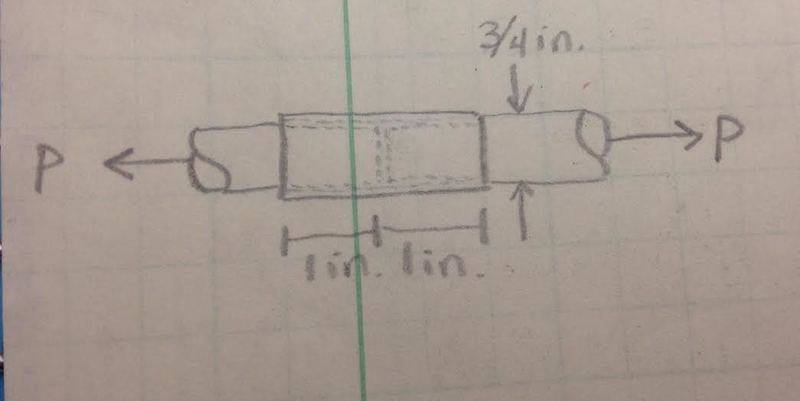
I need help with this problem. I know that {average shear stress} = {force} / {area}. But I am very confused when you take into account this splicing! Thank you in advance!
Two 3/4-in.-diameter nylon rods are spliced together by gluing a 2-in. section of plastic pipe over the rod ends, as shown in the figure. If a tensile force of P = 500 lb is applied to the spliced nylon rod, what is the average shear stress in the glue going between the pipe and rods?
Figure:
I need help with this problem. I know that {average shear stress} = {force} / {area}. But I am very confused when you take into account this splicing! Thank you in advance!