Automorphisms of Field Extensions .... Lovett, Example 11.1.8

[Math Amateur]

I am reading "Abstract Algebra: Structures and Applications" by Stephen Lovett ...

I am currently focused on Chapter 8: Galois Theory, Section 1: Automorphisms of Field Extensions ... ...

I need help with Example 11.1.8 on page 559 ... ...Example 11.1.8 reads as follows:

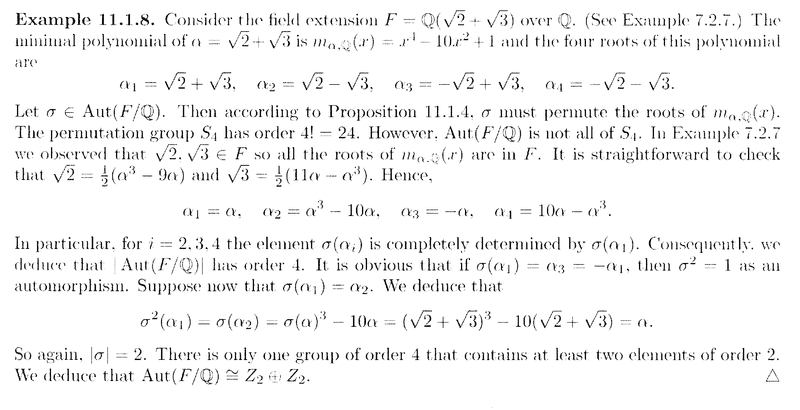
My questions regarding the above example from Lovett are as follows:
Question 1In the above text from Lovett we read the following:" ... ... The minimal polynomial of ##\alpha = \sqrt{2} + \sqrt{3}## is ##m_{ \alpha , \mathbb{Q} } (x) = x^4 - 10x^2 + 1## and the four roots of this polynomial are##\alpha_1 = \sqrt{2} + \sqrt{3}, \ \ \alpha_2 = \sqrt{2} - \sqrt{3}, \ \ \alpha_3 = - \sqrt{2} + \sqrt{3}, \ \ \alpha_4 = - \sqrt{2} - \sqrt{3} ##

... ... ... ... "
Can someone please explain why, exactly, these are roots of the minimum polynomial ##m_{ \alpha , \mathbb{Q} } (x) = x^4 - 10x^2 + 1## ... ... and further, how we would go about methodically determining these roots to begin with ... ...

Question 2In the above text from Lovett we read the following:" ... ... Let ##\sigma \in \text{ Aut}(F/ \mathbb{Q} )##. Then according to Proposition 11.1.4, ##\sigma## must permute the roots of ##m_{ \alpha , \mathbb{Q} } (x)## ... ... "Can someone explain what this means ... how exactly does ##\sigma## permute the roots of ##m_{ \alpha , \mathbb{Q} } (x)## ... ... and how does Proposition 11.1.4 assure this, exactly ... ...
NOTE: The above question refers to Proposition 11.1.4 so I am providing that proposition and its proof ... ... as follows:

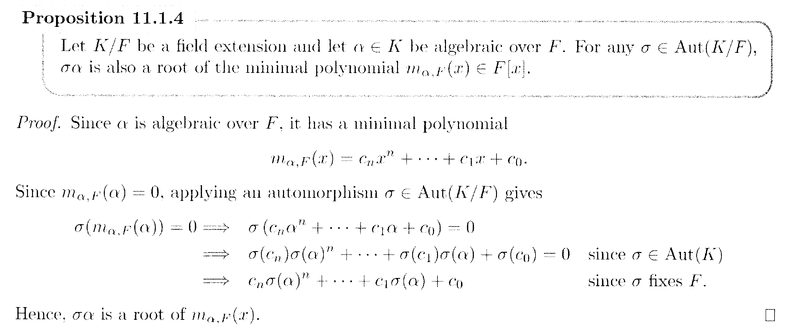
Question 3In the above text from Lovett we read the following:" ... ... In Example 7.2.7 we observed that ##\sqrt{2}, \sqrt{3} \in F## so all the roots of ##m_{ \alpha , \mathbb{Q} } (x)## are in ##F## ... ... "Can someone please explain in simple terms exactly why and how we know that ##\sqrt{2}, \sqrt{3} \in F## ... ... ?
NOTE: Lovett mentions Example 7.2.7 so I am providing the text of this example ... as follows:

I hope that someone can help with the above three questions ...

Any help will be much appreciated ... ...

Peter

 

[fresh_42]

Hi Peter,

concerning your first question. What do you know about ##\alpha := \sqrt{2}+\sqrt{3}## ?

If there is nothing given or known otherwise, you could start and calculate ##\alpha^2, \alpha^3, \alpha^4##. After that, one sees, that ##\alpha^4 -10 \alpha^2 +1 = 0## which makes the minimal polynomial a divisor of ##f(x) = x^4-10x^2+1##. Next you can divide ##g(x) = f(x) : (x-\alpha)## which gives you a polynomial of degree three, which you could solve either by the formula for such polynomials or by guessing another root ##\beta##, divide ##h(x) = g(x) : (x-\beta)## and solve the quadratic equation ##h(x)=0## to get the remaining two roots.

The easier way is experience. If you regard elements like ##\sqrt{-1}\; , \;\sqrt{2}## or similar, the conjugate negative root is always the other root of their minimal polynomials. So it is an educated guess to assume at least ##-\sqrt{2} - \sqrt{3}## as another root. The other two are similar combined from the conjugates. It is rather unlikely that the other roots are completely different. So usually one "guesses" those roots instead of the long calculation I described above and simply multiply ##(\sqrt{2} + \sqrt{3})(-\sqrt{2} - \sqrt{3})(\sqrt{2} - \sqrt{3})(-\sqrt{2} + \sqrt{3})## and see what the result looks like. As none of these are in ##\mathbb{Q}##, the polynomial is separable and irreducible over ##\mathbb{Q}##, which means it is the minimal polynomial (no factors in ##\mathbb{Q}[x]## available).

For your second question:
What happens if you apply a (field) automorphism of ##\sigma \in \operatorname{Aut}(F/K)## to
$$m_{\alpha_1,K}(x) = x^n + a_{n-1}x^{n-1}+ \ldots + a_1x+a_0 = (x-\alpha_1)\cdot \ldots \cdot (x-\alpha_n)$$
What can you say about ##m_{\alpha,K}(\sigma(\alpha_1))## ?

The answer to your third question is already contained in exercise 11.1.8.
If you have done the long calculation with ##\alpha, \alpha^2,\alpha^3,\alpha^4## you can see what ##\alpha^3-11\alpha## and ##\alpha^3-9\alpha## with ##\alpha = \sqrt{2}+\sqrt{3}## gets you. Or simply calculate these powers now and try to find equations ##\sqrt{2} = ...## and ##\sqrt{3} = ...## in terms of these powers of ##\alpha##. Or you take a look on what Lovett has written in exercise 11.1.8.

 

[Math Amateur]

Hi Peter,

concerning your first question. What do you know about ##\alpha := \sqrt{2}+\sqrt{3}## ?

If there is nothing given or known otherwise, you could start and calculate ##\alpha^2, \alpha^3, \alpha^4##. After that, one sees, that ##\alpha^4 -10 \alpha^2 +1 = 0## which makes the minimal polynomial a divisor of ##f(x) = x^4-10x^2+1##. Next you can divide ##g(x) = f(x) : (x-\alpha)## which gives you a polynomial of degree three, which you could solve either by the formula for such polynomials or by guessing another root ##\beta##, divide ##h(x) = g(x) : (x-\beta)## and solve the quadratic equation ##h(x)=0## to get the remaining two roots.

The easier way is experience. If you regard elements like ##\sqrt{-1}\; , \;\sqrt{2}## or similar, the conjugate negative root is always the other root of their minimal polynomials. So it is an educated guess to assume at least ##-\sqrt{2} - \sqrt{3}## as another root. The other two are similar combined from the conjugates. It is rather unlikely that the other roots are completely different. So usually one "guesses" those roots instead of the long calculation I described above and simply multiply ##(\sqrt{2} + \sqrt{3})(-\sqrt{2} - \sqrt{3})(\sqrt{2} - \sqrt{3})(-\sqrt{2} + \sqrt{3})## and see what the result looks like. As none of these are in ##\mathbb{Q}##, the polynomial is separable and irreducible over ##\mathbb{Q}##, which means it is the minimal polynomial (no factors in ##\mathbb{Q}[x]## available).

For your second question:
What happens if you apply a (field) automorphism of ##\sigma \in \operatorname{Aut}(F/K)## to
$$m_{\alpha_1,K}(x) = x^n + a_{n-1}x^{n-1}+ \ldots + a_1x+a_0 = (x-\alpha_1)\cdot \ldots \cdot (x-\alpha_n)$$
What can you say about ##m_{\alpha,K}(\sigma(\alpha_1))## ?

The answer to your third question is already contained in exercise 11.1.8.
If you have done the long calculation with ##\alpha, \alpha^2,\alpha^3,\alpha^4## you can see what ##\alpha^3-11\alpha## and ##\alpha^3-9\alpha## with ##\alpha = \sqrt{2}+\sqrt{3}## gets you. Or simply calculate these powers now and try to find equations ##\sqrt{2} = ...## and ##\sqrt{3} = ...## in terms of these powers of ##\alpha##. Or you take a look on what Lovett has written in exercise 11.1.8.

Thanks for the post, fresh_42 ...

It was most helpful ...

Will check the approaches and calculations that you mention ...

Peter

 

[Math Amateur]

Hi Peter,

concerning your first question. What do you know about ##\alpha := \sqrt{2}+\sqrt{3}## ?

If there is nothing given or known otherwise, you could start and calculate ##\alpha^2, \alpha^3, \alpha^4##. After that, one sees, that ##\alpha^4 -10 \alpha^2 +1 = 0## which makes the minimal polynomial a divisor of ##f(x) = x^4-10x^2+1##. Next you can divide ##g(x) = f(x) : (x-\alpha)## which gives you a polynomial of degree three, which you could solve either by the formula for such polynomials or by guessing another root ##\beta##, divide ##h(x) = g(x) : (x-\beta)## and solve the quadratic equation ##h(x)=0## to get the remaining two roots.

The easier way is experience. If you regard elements like ##\sqrt{-1}\; , \;\sqrt{2}## or similar, the conjugate negative root is always the other root of their minimal polynomials. So it is an educated guess to assume at least ##-\sqrt{2} - \sqrt{3}## as another root. The other two are similar combined from the conjugates. It is rather unlikely that the other roots are completely different. So usually one "guesses" those roots instead of the long calculation I described above and simply multiply ##(\sqrt{2} + \sqrt{3})(-\sqrt{2} - \sqrt{3})(\sqrt{2} - \sqrt{3})(-\sqrt{2} + \sqrt{3})## and see what the result looks like. As none of these are in ##\mathbb{Q}##, the polynomial is separable and irreducible over ##\mathbb{Q}##, which means it is the minimal polynomial (no factors in ##\mathbb{Q}[x]## available).

For your second question:
What happens if you apply a (field) automorphism of ##\sigma \in \operatorname{Aut}(F/K)## to
$$m_{\alpha_1,K}(x) = x^n + a_{n-1}x^{n-1}+ \ldots + a_1x+a_0 = (x-\alpha_1)\cdot \ldots \cdot (x-\alpha_n)$$
What can you say about ##m_{\alpha,K}(\sigma(\alpha_1))## ?

The answer to your third question is already contained in exercise 11.1.8.
If you have done the long calculation with ##\alpha, \alpha^2,\alpha^3,\alpha^4## you can see what ##\alpha^3-11\alpha## and ##\alpha^3-9\alpha## with ##\alpha = \sqrt{2}+\sqrt{3}## gets you. Or simply calculate these powers now and try to find equations ##\sqrt{2} = ...## and ##\sqrt{3} = ...## in terms of these powers of ##\alpha##. Or you take a look on what Lovett has written in exercise 11.1.8.

Thanks again for the help fresh_42 ...

Regarding question 2 you write ...

" ... ...
What happens if you apply a (field) automorphism of ##\sigma \in \operatorname{Aut}(F/K)## to
$$m_{\alpha_1,K}(x) = x^n + a_{n-1}x^{n-1}+ \ldots + a_1x+a_0 = (x-\alpha_1)\cdot \ldots \cdot (x-\alpha_n)$$... ... "As Lovett points out in the proof of Proposition 11.1.4 applying ##\sigma \in \text{Aut} (F/K)## to gives

##\sigma ( m_{ \alpha , K} ( \alpha ) ) = 0 ##

##\Longrightarrow c_n \sigma ( \alpha )^n + \ ... \ ... \ + c_1 \sigma ( \alpha ) + c_0 = 0##

giving the result that ##\sigma \alpha## is a root of ##m_{ \alpha , K} (x)## ...But what is ##m_{ \alpha , K} ( \sigma ( \alpha_1 ) ) ## ? I am not sure ... how do we determine it ... ?

Is ##m_{ \alpha , K} ( \sigma ( \alpha_1 ) ) ## the same as ##\sigma \ m_{ \alpha , K} ( \alpha_1 )## ?Can you help ... I somewhat lost ...

Peter

 

[fresh_42]

\subseteq

" ... ...
What happens if you apply a (field) automorphism of ##\sigma \in \operatorname{Aut}(F/K)## to
$$m_{\alpha_1,K}(x) = x^n + a_{n-1}x^{n-1}+ \ldots + a_1x+a_0 = (x-\alpha_1)\cdot \ldots \cdot (x-\alpha_n)$$... ... "

As Lovett points out in the proof of Proposition 11.1.4 applying ##\sigma \in \text{Aut} (K/F)## to gives
##\sigma ( m_{ \alpha , F} ( \alpha ) ) = 0 ##

This is a basic and important part of the definition, resp. construction of ##\operatorname{Aut}(K/F)##.
An element ##\sigma## of this group, satisfies

• ##\sigma(a+b)=\sigma(a)+\sigma(b)##
  
• ##\sigma(a\cdot b) = \sigma(a) \cdot \sigma(b)##
• ##\sigma(f)=f## for all ##f\in F##

I mistakenly swapped ##F## and ##K## in post #2 compared to Lovett's notation, sorry. So here it is ##F \subseteq K##.
Especially the third property is important for the minimal polynomials. It says that automorphisms from ##\operatorname{Aut}(K/F)## leave all elements of ##F## invariant, fixed, unchanged or whatever you like to call it. Since ##m_{\alpha ,F}(x) \in F[x]##, we get ##\sigma(m_{\alpha ,F}(x))=m_{\alpha ,F}(x)\,##. If you like you can write this as
$$\sigma(m_{\alpha ,F}(x)) = \sigma(a_nx^n+\ldots +a_0)=a_n \sigma(x)^n + \ldots + a_1 \sigma(x) + a_0 = m_{\alpha ,F}(\sigma(x)) = m_{\alpha ,F}(y)$$
with ##y=\sigma(x)## by the help of the properties above and rename the variable ##y=x## again. Of course this is a bit of a nonsense, as ##\sigma## doesn't have anything to do with ##x## and ##\sigma(x)## isn't even defined. Formally we would have to extend ##\sigma ## to a ring homomorphism ##\overline{\sigma}## of ## F[x]## first, and then show, that it is the identity. However, it should only stress, that ##\sigma## leaves the polynomials from ##F[x]## unchanged, or to be exact ## \overline{\sigma}(m_{\alpha ,F}(x)) = m_{\alpha ,F}(x)##. If it confuses you, forget this little detour again. You might as an alternative also look at polynomials as elements ##(a_0,a_1,\ldots ,a_n) \in F^n##, i.e. the ordered tuples of its coefficients. In this notation, the third property above shows immediately the invariance of them under ##\sigma##. Anyway, important alone are the following equations
$$
\sigma(m_{\alpha ,F}(c)) \stackrel{(*)}{=} m_{\alpha ,F}(c) \text{ for all } c \in F \text{ and } \sigma(m_{\alpha ,F}(k)) \stackrel{(*)}{=} m_{\alpha ,F}(\sigma(k)) \text{ for all } k \in K
$$
Now if we write the minimal polynomial in its split form in ##K[x]##, we get from ##(*)##
\begin{equation}
\overline{\sigma}(m_{\alpha ,F}(x) =\overline{\sigma} \left( (x-\alpha_1) \cdot \ldots \cdot (x-\alpha_n) \right) = (x-\sigma(\alpha_1)) \cdot \ldots \cdot (x-\sigma(\alpha_n)) = m_{\alpha ,F}(x) = (x-\alpha_1) \cdot \ldots \cdot (x-\alpha_n)
\end{equation}
which shows that ##\{c \in F\,\vert \, m_{\alpha ,F}(c)= 0\} = \{c \in F\,\vert \, m_{\alpha ,F}(\sigma(c))= 0\}##. As this is a finite set, the only possibility is a shuffle of zeros, i.e. a permutation of them.

I guess this or similar is how Lovett has proven his proposition 11.1.4.

##\Longrightarrow c_n \sigma ( \alpha )^n + \ ... \ ... \ + c_1 \sigma ( \alpha ) + c_0 = 0##

giving the result that ##\sigma \alpha## is a root of ##m_{ \alpha , K} (x)## ...But what is ##m_{ \alpha , K} ( \sigma ( \alpha_1 ) ) ## ? I am not sure ... how do we determine it ... ?

Is ##m_{ \alpha , K} ( \sigma ( \alpha_1 ) ) ## the same as ##\sigma \ m_{ \alpha , K} ( \alpha_1 )## ?

There is no secret behind. The moment I wrote ##m_{\alpha ,F}(x) = (x-\alpha_1) \cdot \ldots \cdot (x-\alpha_n)## in ##K[x]## in its decomposed form, I also had numbered all roots ##\alpha_1 , \ldots , \alpha_n##. Since ##\alpha ## is one of them, I had chosen ##\alpha = \alpha_1##. If I had written ##\alpha ## instead, you might have asked, what ##\alpha ## is, as the zeros are all numbered.

I recognize that I start to confuse myself by the attempt to shortcut ##\overline{\sigma}## so I better stop. A summary is:

Because ##\sigma \in \operatorname{Aut}(K/F)## leaves all elements of ##F## pointwise unchanged, it leaves all polynomials with coefficents in ##F## unchanged and especially the minimal polynomial ##m_{\alpha, F}(x)##.
However, ##\sigma## does change the elements of ##K##, so all zeros ##\alpha \in K## of it are changed. But as the polynomial as a whole is the same, the decomposition into factors ##(x-\alpha_i)## shows, that the zeros can only be shuffled.

 

[Math Amateur]

\subseteq
This is a basic and important part of the definition, resp. construction of ##\operatorname{Aut}(K/F)##.
An element ##\sigma## of this group, satisfies

• ##\sigma(a+b)=\sigma(a)+\sigma(b)##
  
• ##\sigma(a\cdot b) = \sigma(a) \cdot \sigma(b)##
• ##\sigma(f)=f## for all ##f\in F##

I mistakenly swapped ##F## and ##K## in post #2 compared to Lovett's notation, sorry. So here it is ##F \subseteq K##.
Especially the third property is important for the minimal polynomials. It says that automorphisms from ##\operatorname{Aut}(K/F)## leave all elements of ##F## invariant, fixed, unchanged or whatever you like to call it. Since ##m_{\alpha ,F}(x) \in F[x]##, we get ##\sigma(m_{\alpha ,F}(x))=m_{\alpha ,F}(x)\,##. If you like you can write this as
$$\sigma(m_{\alpha ,F}(x)) = \sigma(a_nx^n+\ldots +a_0)=a_n \sigma(x)^n + \ldots + a_1 \sigma(x) + a_0 = m_{\alpha ,F}(\sigma(x)) = m_{\alpha ,F}(y)$$
with ##y=\sigma(x)## by the help of the properties above and rename the variable ##y=x## again. Of course this is a bit of a nonsense, as ##\sigma## doesn't have anything to do with ##x## and ##\sigma(x)## isn't even defined. Formally we would have to extend ##\sigma ## to a ring homomorphism ##\overline{\sigma}## of ## F[x]## first, and then show, that it is the identity. However, it should only stress, that ##\sigma## leaves the polynomials from ##F[x]## unchanged, or to be exact ## \overline{\sigma}(m_{\alpha ,F}(x)) = m_{\alpha ,F}(x)##. If it confuses you, forget this little detour again. You might as an alternative also look at polynomials as elements ##(a_0,a_1,\ldots ,a_n) \in F^n##, i.e. the ordered tuples of its coefficients. In this notation, the third property above shows immediately the invariance of them under ##\sigma##. Anyway, important alone is the following equations
$$
\sigma(m_{\alpha ,F}(c)) \stackrel{(*)}{=} m_{\alpha ,F}(c) \text{ for all } c \in F \text{ and } \sigma(m_{\alpha ,F}(k)) \stackrel{(*)}{=} m_{\alpha ,F}(\sigma(k)) \text{ for all } k \in K
$$
Now if we write the minimal polynomial in its split form in ##K[x]##, we get from ##(*)##
\begin{equation}
\overline{\sigma}(m_{\alpha ,F}(x) =\overline{\sigma} \left( (x-\alpha_1) \cdot \ldots \cdot (x-\alpha_n) \right) = (x-\sigma(\alpha_1)) \cdot \ldots \cdot (x-\sigma(\alpha_n)) = m_{\alpha ,F}(x) = (x-\alpha_1) \cdot \ldots \cdot (x-\alpha_n)
\end{equation}
which shows that ##\{c \in F\,\vert \, m_{\alpha ,F}(c)= 0\} = \{c \in F\,\vert \, m_{\alpha ,F}(\sigma(c))= 0\}##. As this is a finite set, the only possibility is a shuffle of zeros, i.e. a permutation of them.

I guess this or similar is how Lovett has proven his proposition 11.1.4.

There is no secret behind. The moment I wrote ##m_{\alpha ,F}(x) = (x-\alpha_1) \cdot \ldots \cdot (x-\alpha_n)## in ##K[x]## in its decomposed form, I also had numbered all roots ##\alpha_1 , \ldots , \alpha_n##. Since ##\alpha ### is one of them, I had chosen ##\alpha = \alpha_1##. If I had written ##\alpha ## instead, you might have asked, what ##\alpha ## is, as the zeros are all numbered.

I recognize that I start to confuse myself by the attempt to shortcut ##\overline{\sigma}## so I better stop. A summary is:

Because ##\sigma \in \operatorname{Aut}(K/F)## leaves all elements of ##F## pointwise unchanged, it leaves all polynomials with coefficents in ##F## unchanged and especially the minimal polynomial ##m_{\alpha, F}(x)##.
However, ##\sigma## does change the elements of ##K##, so all zeros ##\alpha \in K## of it are changed. But as the polynomial as a whole is the same, the decomposition into factors ##(x-\alpha_i)## shows, that the zeros can only be shuffled.

Thanks so much fresh_42 ... that was very helpful ...

Seems much clearer now ... but still spending time re-reading your post and reflecting on what you have said...

Thanks again for your help and support... it is much appreciated...

Peter