- #1
karush
Gold Member
MHB
- 3,269
- 5
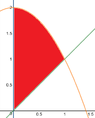
$\textsf{Find the center of mass of a thin plate of density}$
$\textsf{ $\delta=3$ bounded by the lines $x=0, y=x$, and the parabola
$y=2-x^2$ in the $Q1$}$
$\begin{array}{llcr}\displaystyle
&\textit{Mass}\\
&&\displaystyle M=\iint\limits_{R}\delta \, dA\\
&\textit{First Moments}\\
&&\displaystyle M_y=\iint\limits_{R}x\delta \, dA
&\displaystyle M_x=\iint\limits_{R}y\delta \, dA\\
&\textit{Center of mass}\\
&&\displaystyle\bar{x}=\displaystyle\frac{M_y}{M},
\displaystyle\bar{y}=\displaystyle\frac{M_x}{M}\\
\\
&&\color{red}
{\displaystyle \, \bar{x}=\frac{5}{14},
\bar{y}=\displaystyle\frac{38}{35}}\\
\end{array}$ok I just barely had to time to post this
equations are just from reference
red is answer
$\textsf{ $\delta=3$ bounded by the lines $x=0, y=x$, and the parabola
$y=2-x^2$ in the $Q1$}$
$\begin{array}{llcr}\displaystyle
&\textit{Mass}\\
&&\displaystyle M=\iint\limits_{R}\delta \, dA\\
&\textit{First Moments}\\
&&\displaystyle M_y=\iint\limits_{R}x\delta \, dA
&\displaystyle M_x=\iint\limits_{R}y\delta \, dA\\
&\textit{Center of mass}\\
&&\displaystyle\bar{x}=\displaystyle\frac{M_y}{M},
\displaystyle\bar{y}=\displaystyle\frac{M_x}{M}\\
\\
&&\color{red}
{\displaystyle \, \bar{x}=\frac{5}{14},
\bar{y}=\displaystyle\frac{38}{35}}\\
\end{array}$ok I just barely had to time to post this
equations are just from reference
red is answer