The Fundamental Theorem of Algebra

In summary, the conversation is about a polynomial of the form a^n where a0 ≠ 0, meaning it is a genuine nth-degree polynomial. The conversation also includes a discussion about using Latex and some playful banter between the participants.
  • #1
SprucerMoose
62
0
Hi all,
I'm currently flicking through and old textbook and came across the following.

"Every polynomial of the form
P(z)%20=%20a_{0}x^{n}%20+%20a_{1}x^{n-1}%20+%20a_{2}x^{n-2}%20+%20...%20+%20a_{n-1}x%20+%20a_{n}.gif
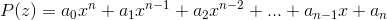, where
gif.latex?a^{n}\neq0.gif
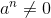has n linear factors over C...". What does it mean by [URL]http://latex.codecogs.com/gif.latex?a^{n}\neq0?[/URL] Is this referring to some kind of complex index? This is all that is written and nothing precedes it. I just don't quite understand the
gif.latex?a^{n}\neq0.gif
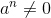.Edit: Latex kind of fixed
 
Last edited by a moderator:
Mathematics news on Phys.org
  • #2
Hi SprucerMoose! :smile:

(try using the X2 and X2 icons just above the Reply box :wink:)

it must be a misprint for "where a0 ≠ 0" …

in other words, where it's a genuine nth-degree polynomial :smile:
 
  • #3
Ah, I see. Thank you very much.Testing...

a2 + a0 + a1

Edit: It works!
 
  • #4
SprucerMoose said:
Testing...

a2 + a0 + a1

Edit: It works!

Now you really are sprucer! :biggrin:
 
  • #5
SprucerMoose said:
Ah, I see. Thank you very much.


Testing...

a2 + a0 + a1

Edit: It works!
Do you mean a2 + a0 + a1?
 
  • #6
Mark44 said:
Do you mean a2 + a0 + a1?

Do you mean a2 + a0 + a1?
 
  • #7
Top that! :smile:

SprucerMoose wins! :biggrin:​
 

Related to The Fundamental Theorem of Algebra

What is the Fundamental Theorem of Algebra?

The Fundamental Theorem of Algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root.

Why is the Fundamental Theorem of Algebra important?

The Fundamental Theorem of Algebra is important because it provides a powerful tool for solving polynomial equations, which are used in many areas of mathematics and science. It also helps to understand the structure of the complex numbers and their relationship to polynomials.

How was the Fundamental Theorem of Algebra proven?

The Fundamental Theorem of Algebra was proven by Carl Friedrich Gauss in 1799. He used complex analysis and the concept of analytic continuation to show that any non-constant polynomial with complex coefficients can be factored into linear or quadratic terms, which must have complex roots.

Can the Fundamental Theorem of Algebra be applied to all polynomials?

Yes, the Fundamental Theorem of Algebra applies to all non-constant single-variable polynomials with complex coefficients. It does not apply to polynomials with coefficients in other number systems, such as the rational numbers or the real numbers.

What are some real-world applications of the Fundamental Theorem of Algebra?

The Fundamental Theorem of Algebra has many real-world applications, including in engineering, physics, economics, and computer science. It is used to solve polynomial equations in various fields, such as circuit design, signal processing, and optimization problems. It also has applications in data analysis and cryptography.

Similar threads

B Extending the Fundamental Theorem of Arithmetic to the rationals
    • General Math
2
Replies
35
Views
3K
I Question about the Fundamental Theorem of Algebra
    • General Math
Replies
14
Views
2K
Fundamental theorem of algebra and factoring?
    • General Math
Replies
6
Views
1K
So-called Fundamental Theorem of Algebra
    • General Math
Replies
1
Views
1K
B Confusion about The Conjugate Roots Theorem
    • General Math
Replies
8
Views
1K
I If pair of polynomials have Greatest Common Factor as 1 ....
    • General Math
Replies
1
Views
1K
I Prove an nth-degree polynomial has exactly n roots
    • General Math
Replies
3
Views
6K
Python’s Sympy Module and the Cayley-Hamilton Theorem
    • Programming and Computer Science
Replies
1
Views
2K
I Fundamental representation and adjoint representation
    • Quantum Physics
Replies
27
Views
1K
I On the topological proof of the Fundamental Theorem of Algebra
    • Topology and Analysis
Replies
18
Views
3K

Hot Threads

Recent Insights

Back
Top