- #1
Happiness
- 679
- 30
The attachment below proves that an nth-degree polynomial has exactly ##n## roots.
The outline of the proof is as follows:
Suppose (1.1) has ##r## roots. Then it can be written in the form of (1.8) by factor theorem.
Next use the second fundamental result in algebra (SFRA): if ##f(x)=F(x)## for all values of ##x##, then their coefficients ##a_i##'s in (1.1) are the same. So we have [after expanding (1.8)] ##Ax^r=a_nx^n##. Thus ##r=n##.
The last sentence suggests that if ##f(x)## can be written in the form (1.8) then the proof is complete. And it can be by factor theorem.
My issue with the proof is that the condition for SFRA is not satisfied and hence we cannot compare the coefficients ##a_i##'s. We do not know that ##f(x)=F(x)## for all values of ##x##; we only know ##f(x)=F(x)## for ##r## values of ##x##, for those ##r## roots ##\alpha_i##'s.
So how could we justify the use of SFRA?
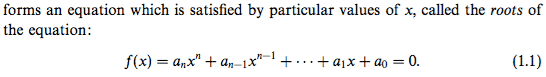

The outline of the proof is as follows:
Suppose (1.1) has ##r## roots. Then it can be written in the form of (1.8) by factor theorem.
Next use the second fundamental result in algebra (SFRA): if ##f(x)=F(x)## for all values of ##x##, then their coefficients ##a_i##'s in (1.1) are the same. So we have [after expanding (1.8)] ##Ax^r=a_nx^n##. Thus ##r=n##.
The last sentence suggests that if ##f(x)## can be written in the form (1.8) then the proof is complete. And it can be by factor theorem.
My issue with the proof is that the condition for SFRA is not satisfied and hence we cannot compare the coefficients ##a_i##'s. We do not know that ##f(x)=F(x)## for all values of ##x##; we only know ##f(x)=F(x)## for ##r## values of ##x##, for those ##r## roots ##\alpha_i##'s.
So how could we justify the use of SFRA?
Last edited: