Energy stored in an electrostatic system

[Pushoam]

<Moderator's note: Thread moved from a technical forum, so homework template missing>

To do: To find an expression for energy stored in an electrostatic system with charge density ## \rho ## and volume R.
[ I am using R to denote the region filled with the given charge density as I want to keep 'V' reserved for potential ].

By the term "energy of the system " what we mean is : work required to assemble the system

So, I have to calculate work required to assemble the system i.e. W.

Let's consider the system at the time when its volume is Δ R and I bring charge dq to a point M with position vector ##\vec r ## on its surface.

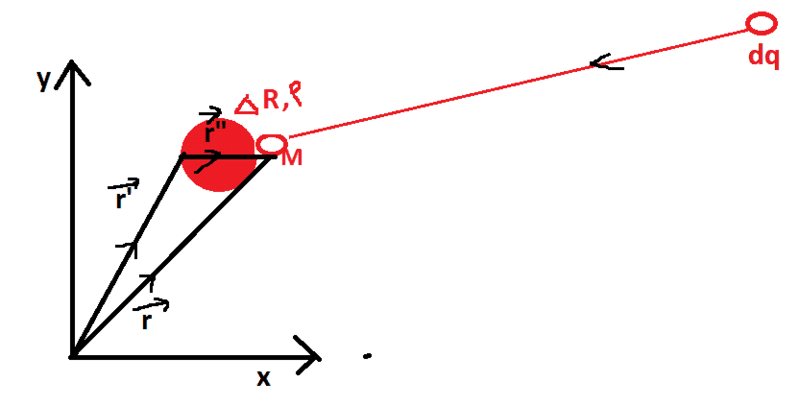
Work done by me in this process is
dW = V(##\vec r ##) dq

##V \left ( \vec r \right ) = k \int _{ΔR}~ \frac { \rho (\vec {r'}) }{r"} d \, τ' ##
## dq = \rho (\vec {r}) dτ ##
So, ## dW = k \int _R~ \frac { \rho (\vec {r'}) }{r"} d \, τ' ~ \rho (\vec {r}) dτ ##
## W = \int _R~ \rho (\vec {r}) \{ k \int _{ΔR}~ \frac { \rho (\vec {r'}) }{r"} d \, τ'\} d\,τ ##

where ΔR depends on r.

Is this correct so far?

Another way:

W = ½ ##\int_R ~ \rho (\vec r) V (\vec r) d \, τ##
## \rho (\vec r) V (\vec r) = ε_0 (∇⋅ \vec E ) V = ε_0 ( ∇⋅( V \vec E ) - \vec E⋅ ∇ V ) ##
## W = ½ \int_R~ ε_0 ( ∇⋅ (V \vec E ) - \vec E⋅ ∇ V ) d \,τ ##
## = ½ \int_S ~ ε_0 V \vec E ⋅ d \vec a + ½ \int_R ε_0 E^2 d \, τ ##
Taking the region of integration to be infinite, (as the charge density outside R is 0), the first integral on R.H.S. becomes 0. Hence, we have,
## W = \frac {\epsilon _0 } 2 \int_{all space} E^2 d \, \tau ##In case of dielectrics, this will be the work required for assembling both free charges and bound charges.

For dielectrics, ## \rho = \rho_b + \rho_f,##
So,
W = ½ ##\int_R ~ \rho (\vec r) V (\vec r) d \, τ##
= ½ ##\int_R~ (\rho_b + \rho_f )V (\vec r) d \, τ##
W =½ ## \int_R~ \rho_b V d \, τ + ½ \int_R \rho_f V (\vec r) d \, τ##

Can I take the first term on the R.H.S. as the work required to assemble the bound charges and the second term as the work required to assemble the free charges ?

If yes, then,

##W_f = ½ \int_R \rho_f V (\vec r) d \, τ
\\ \rho_f=∇.\vec D##
And doing some further calculation,
## W_f = ½ \int_{all space} \vec D . \vec E ~d \, τ ##

Is this correct so far?

 

[Pushoam]

Calculating work done required in building free charges up from zero to the final configuration in dielectrics

Here, the volume of the system( dielectrics ) R is fixed. So, as I bring free charge Δq to the system, its free charge density ## \rho_f ## gets changed by ##Δ \rho_f ##. Change in free charge density creates change in bound charge density ( only ## \rho_b ## or both## \rho_b## and ##σ_b## ?).

##Δq = \int_R (ρ_f + Δ ρ_f ) d \, τ - \int_R ρ_f d \, τ = \int_R Δρ_f d \, τ ##Work done on bringing this incremental charge from infinity to a point with position vector ## \vec r ## inside the dielectrics is

##ΔW = Δq V(\vec r )## (1)

## ΔW = V(\vec r ) \int_R Δρ_f d \, τ ## (1.1)

But, the Griffith says in eq. 4.56 3rd ed. : ## ΔW = \int_R Δρ_f V(\vec r ) d \, τ ##
So, something may be wrong in (1).
I think Δq gets spread in all over the dielectrics. It doesn't remain at ## \vec r ## in the dielectrics.
So, eq (1) has to be modified.
Let's say that a very small amount of Δq i.e. Δ (Δq) remains at ## \vec r ## after the spreading. Now, work done on this charge is

##Δ(ΔW) = Δ(Δq) V( \vec r )##

On integrating both sides,

## ΔW = Δ\int _R Δ(Δρ_f) V(\vec r ) d \, τ ##

This also doesn't match the Griffith's expression.
I guess the way Griffith's brings the free charge is following:
He doesn't bring the charge Δq at ## \vec r ##. He brings the charge Δq over all the region of dielectrics simultaneously so that its free charge density gets increased by ## Δρ_f ##. Now, ##Δ ρ_f (\vec r ) V(\vec r ) d \, τ ## is the work done in bringing the charge ## Δ ρ_f (\vec r ) d \, τ ## at ## \vec r ##. Hence, the work done in bringing Δq all over the dielectrics is

## ΔW = \int _R~ Δ ρ_f (\vec r ) ~ V(\vec r ) d \, τ ##

Where ## V (\vec r )## is potential due to the system at ## \vec r## at the time when the charge ## Δ ρ_f (\vec r ) d \, τ ## is brought to ## \vec r##.

## Δρ_f = ∇ρ_f ⋅ d \vec r = ∇ (∇⋅ \vec D )⋅ d \vec r##

Now, Griffiths takes ## Δ ρ_f = ∇. (Δ \vec D ) ##.
This means,
## \begin {align}
Δρ_f & = Δ (∇. \vec D ) & = ∇. (Δ \vec D )
\\& ⇒ [ ∇(∇. \vec D)]. d \vec r & = ∇. ( ∇ D_j .d \vec r ) \hat x_j
\\ & ⇒ \frac { \partial { [ \frac {\partial D_j } {\partial x_j } ] } } {\partial {x_i } } d x_i & = \frac { \partial { [ \frac {\partial D_j } {\partial x_k } d x_k ] } } {\partial {x_j } }
\end {align} ##

How to prove the equality in the last equation?

Since I understand the following steps, I am copying it from Griffiths.

Now, since we have to calculate W instead of ΔW, what Griffith does is : ## (Δ \vec D ) . \vec E = \frac {Δ(\vec D .\vec E )} 2 ##

This I can show as following:

## (Δ \vec D ) . \vec E = E_i (∇ D_i . d\vec r ) = \frac { Δ (E_i D_i )} 2 = \frac {Δ(\vec D .\vec E )} 2 ##

while taking the integration over all space, it is assumed that space outside R is vacuum.
Is this assumption necessary?

Now, Griffith takes Δ outside the integration. Can anyone please explain me how can one show the correctness of this step?

Can anyone please explain me the underlined part in the following footnote?

I am attaching Griffith's derivation of eqn. 2.42 and 4.58 given in 3rd ed.