What is Field: Definition and 1000 Discussions

In mathematics, a field is a set on which addition, subtraction, multiplication, and division are defined and behave as the corresponding operations on rational and real numbers do. A field is thus a fundamental algebraic structure which is widely used in algebra, number theory, and many other areas of mathematics.
The best known fields are the field of rational numbers, the field of real numbers and the field of complex numbers. Many other fields, such as fields of rational functions, algebraic function fields, algebraic number fields, and p-adic fields are commonly used and studied in mathematics, particularly in number theory and algebraic geometry. Most cryptographic protocols rely on finite fields, i.e., fields with finitely many elements.
The relation of two fields is expressed by the notion of a field extension. Galois theory, initiated by Évariste Galois in the 1830s, is devoted to understanding the symmetries of field extensions. Among other results, this theory shows that angle trisection and squaring the circle cannot be done with a compass and straightedge. Moreover, it shows that quintic equations are, in general, algebraically unsolvable.
Fields serve as foundational notions in several mathematical domains. This includes different branches of mathematical analysis, which are based on fields with additional structure. Basic theorems in analysis hinge on the structural properties of the field of real numbers. Most importantly for algebraic purposes, any field may be used as the scalars for a vector space, which is the standard general context for linear algebra. Number fields, the siblings of the field of rational numbers, are studied in depth in number theory. Function fields can help describe properties of geometric objects.

View More On Wikipedia.org
Recent contents Top users
  1. tanaygupta2000

    Electric field inside a spherical cavity inside a dielectric

  2. E

    Electric field within a battery

    I've been reading through this paper to try and get a better understanding of how batteries work. The analysis there is fine (they consider a voltaic cell to charge a capacitor in order to derive ##\Delta V=\varepsilon##, and go via an energy route), but it doesn't really touch upon the fields...
  3. R

    Electric field at (0,0) for this charged square conductor

    Can we assume that square charge resembles a sphere shell, and think like electric field at sphere shell's center is 0.
  4. R

    Possible to network in one's field while learning new science?

    Or at least honing ones scientific skill/knowledge? How would one go about this? NOTE: I am talking about a non-pandemic or otherwise non-emergency condition.
  5. R

    Force field suitable for studying silica crystal

    I need some advice and help please -Is There a two body force field suitable to study silica crystal or alpha quartz crystal? it's okay to gives Approximate results. - Is the BKS force field suitable for silica crystal? - If there are other simple terms of force field for studying the silica...
  6. F

    Non-circular motion of a particle in a perpendicular constant magnetic field

    There's a constant magnetic field B. If a particle is acted on by a force qv*B (* cross) only, and the initial velocity v0 is normal to B, is the motion certainly a circular one (for any m, q, v0)? mv''=qv*B If one solves this equation (vector), it doesn't seem obvious.
  7. sagigever

    Magnetic field in a rotating uniformly-charged infinite cylinder

    I am sure I need to use Amper's law to do that. if I use the equation I mentioned above it easy to calculate the right side of the equation but I have problem how to calculate the path integral. I know from right hand rule that the magnetic field will point at $$Z$$ and the current is in...
  8. cianfa72

    I Parallel transport vs Lie dragging along a Killing vector field

    Hi, I would like to ask for a clarification about the difference between parallel transport vs Lie dragging in the following scenario. Take a vector field ##V## defined on spacetime manifold and a curve ##C## on it. The manifold is endowed with the metric connection (I'm aware of it does exist...
  9. K

    I Quantum Field Operators for Bosons

    Consider the field creation operator ψ†(x) = ∫d3p ap†exp(-ip.x) My understanding is that this operator does not add particles from a particular momentum state. Rather it coherently (in-phase) adds a particle created from |0> expanded as a superposition of momentum eigenstates states...
  10. Luke2642

    Force & energy in cutting and stretching magnetic field lines?

    I have an ordinary switchable magnet for holding tools to a lathe. It's like a magnetic force gearbox, but I can't quite understand the force multiplication. When placed on a steel surface the switch force is approximately ~5N on both finger and thumb at 1.5cm radius acting over a 3cm arc...
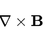
  11. anaisabel

    Magnetic field (correction term)

    Ampere´'s law with the correction term I have a infinite cylinder with radius R with a current density , and magnetic field . I have to proof that it is acceptable to discard the correction term of term of ampere's law, while calculating the magnetic field, as long as it obeys the following...
  12. K

    E&M: Field of a Wire with non-uniform current

    Summary:: Not sure if my solution to a magnetostatics problem is correct [Mentor Note -- thread moved from the technical forums, so no Homework Template is shown] I was trying to solve problem 2 from...
  13. T

    A Evaluating Matrix Spin Dependent Term in Dirac Quadratic Equation

    I derive the quadratic form of Dirac equation as follows $$\lbrace[i\not \partial-e\not A]^2-m^2\rbrace\psi=\lbrace\left( i\partial-e A\right)^2 + \frac{1}{2i} \sigma^{\mu\nu}F_{\mu \nu}-m^2\rbrace\psi=0$$ And I need to find the form of the spin dependent term to get the final expression $$g...
  14. G

    Modulus of the electric field created by a sphere

    I think the right solution is c). I'll pass on my reasoning to you: R=6\, \textrm{cm}=0'06\, \textrm{m} \sigma =\dfrac{10}{\pi} \, \textrm{nC/m}^2=\dfrac{1\cdot 10^{-8}}{\pi}\, \textrm{C/m}^2 P=0'03\, \textrm{m} P'=10\, \textrm{cm}=0,1\, \textrm{m} Point P: \left. \phi =\oint E\cdot...
  15. F

    I Vector field and Helmholtz Theorem

    Hello, A generic vector field ##\bf {F} (r)## is fully specified over a finite region of space once we know both its divergence and the curl: $$\nabla \times \bf{F}= A$$ $$\nabla \cdot \bf{F}= B$$ where ##B## is a scalar field and ##\bf{A}## is a divergence free vector field. The divergence...
  16. G

    Electric field and electric potential exercise

    a) \vec{F}=\vec{E}\cdot q \phi =\oint \vec{E}d\vec{S}=\oint \vec{E}d\vec{S}=\underbrace{\oint \vec{E}d\vec{S}}_{\textrm{FACES } \perp}+\underbrace{\oint \vec{E}d\vec{S}}_{\textrm{FACES } \parallel}=0+\oint EdS\cdot \underbrace{\cos 0}_1= E2S \dfrac{Q_{enc}}{\varepsilon_0}=\phi \left...
  17. E

    Particle motion in a magnetic field

    The equation of motion can be integrated w.r.t. ##t## since ##\frac{d}{dt} (\mathbf{r} \times \mathbf{B}) = \dot{\mathbf{r}} \times \mathbf{B} + \mathbf{0}## $$\int (q\dot{\mathbf{r}} \times \mathbf{B} + m\mathbf{g}) dt = \int m\ddot{\mathbf{r}}(t) dt$$ $$\frac{q}{m} \mathbf{r} \times \mathbf{B}...
  18. Adesh

    I'm not getting the curl of vector potential equal to magnetic field

    In this image of Introduction to Electrodynamics by Griffiths . we have calculated the vector potential as ##\mathbf A = \frac{\mu_0 ~n~I}{2}s \hat{\phi}##. I tried taking its curl but didn't get ##\mathbf B = \mu_0~n~I \hat{z}##. In this thread, I have calculated it like this ...
  19. Adesh

    How to find the curl of a vector field which points in the theta direction?

    I have a vector field which is originallly written as $$ \mathbf A = \frac{\mu_0~n~I~r}{2} ~\hat \phi$$ and I translated it like this $$\mathbf A = 0 ~\hat{r},~~ \frac{\mu_0 ~n~I~r}{2} ~\hat{\phi} , ~~0 ~\hat{\theta}$$(##r## is the distance from origin, ##\phi## is azimuthal angle and ##\theta##...
  20. abivz

    I Obtaining the Dirac function from field operator commutation

    Hi everyone, I'm new to PF and this is my second post, I'm taking a QFT course this semester and my teacher asked us to obtain: $$[\Phi(x,t), \dot{\Phi}(y,t) = iZ\delta^3(x-y)]$$ We're using the Otto Nachtman: Elementary Particle Physics but I've seen other books use this notation: $$[\Phi(x,t)...
  21. abivz

    I QFT - Field operator commutation

    Hi everyone, I'm taking a QFT course this semester and we're studying from the Otto Nachtman: Texts and Monographs in Physics textbook, today our teacher asked us to get to the equation: [Φ(x,t),∂/∂tΦ(y,t)]=iZ∂3(x-y) But I am unsure of how to get to this, does anyone have any advice or any...
  22. P

    Electric field at the center of a sphere

    My first impression was the electric field is 0 at the center of the sphere, but it turned out not the case. My understanding when problems refer surface charge density, is that the charge exists only on the surface and it is hollow inside the sphere. Am i correct? Using the electric field...
  23. T

    Vector Field Transformation to Spherical Coordinates

    I am trying to solve the following problem from my textbook: Formulate the vector field $$ \mathbf{\overrightarrow{a}} = x_{3}\mathbf{\hat{e_{1}}} + 2x_{1}\mathbf{\hat{e_{2}}} + x_{2}\mathbf{\hat{e_{3}}} $$ in spherical coordinates.My solution is the following: For the unit vectors I use the...
  24. dykuma

    Force density from an electromagnetic field

    My guess is that the force per volume is: $$ \vec F_V = \rho \alpha x \hat x + \vec J \times \beta x \hat y$$ but I'm not sure where to go after that. I'm not given a value for either the charge density or the current density, so I can't simplify the relation much. Further, I'm not sure if my...
  25. KC374

    Work Done by an Induced Electric Field

    I have drawn a picture of what the induced electric field will look like, and I have determined its magnitude both within and outside of the magnetic field. I was able to get the right answer for part (b) with this information, but I don't understand why the answer for part (c) is 0 J. It...
  26. P

    Electric field due to a straight rod

    The net electric field is ## 2dE \cos\theta ## ## dE = \lambda dx/(4\pi\epsilon (x^2 +r^2)) \\ 2dE \cos\theta = 2r\lambda dx /(4\pi\epsilon (x^2 +r^2)^\frac 3 2) \\ E_{net} = 2\lambda r /(4\pi\epsilon) \int_0^a dx /( (x^2 +r^2)^\frac 3 2) \\ E_{net} = 2\lambda r /(4\pi\epsilon) [\frac x...
  27. Zero

    Calculating Electric Field: A Failed Attempt

    I tried getting E by dividing volts and distance since I know the distance between the two plates is .352 m but it did not work
  28. P

    Electric Field of a Point Charge and Thin Ring: A Comparative Analysis

    I thought it was easy but i am not getting the correct answer The electric field due the point charge q is ## E1 = q/(4\pi\epsilon x^2) ## The electric field due to the thin ring of radius R is considering the electric field due to the element charge dq (dS) ## dE2 = dq/4\pi\epsilon (x^2 + R^2)...
  29. E

    Nonlinear scalar equation in field theory

    Thank you very much
  30. F

    The orgin of the superposition principle of electric field

    Isn't the superposition principle of electric field just force being addable? Jackson's electrodynamics says it's based on the premise of linear Maxwell's equations. Which support(s) the superposition principle?
  31. Adwit

    A Quantum Field Theory: 3-4 Equation Steps Explained

    I understand how do 3 no. equation come from 1 & 2 no. equation. But I am struggling to understand how do 4 no. equation come from 3 no. equation. Will anyone do the steps between 3 no. equation and 4 no. equation, please ?
  32. E

    Function for the movement of a charged particle in a B field

    The movement in the z-direction is easy to solve for, as it's only affected by the gravitational force. However, if there's a magnetic field pointing down along the z-axis, the particle is going to be accelerated along the y-axis (F=q*v *B). The force is always going to be perpendicular to the...
  33. C

    Parameterize Radial Vector of Electric Field due to Spherical Shell

    Homework statement: Find the electric field a distance z from the center of a spherical shell of radius R that carries a uniform charge density σ. Relevant Equations: Gauss' Law $$\vec{E}=k\int\frac{\sigma}{r^2}\hat{r}da$$ My Attempt: By using the spherical symmetry, it is fairly obvious...
  34. Elder1994

    Magnetic field due to the current flowing in a bent wire

    Hello, in this problem I'm supposed to calculate de magnetic field due to a bent wire at any point of the x-axis after the bending of the wires. It is obvious that the part of the wire that is parallel to the x-axis makes no contribution to the field so we can focus on the other part of the...
  35. E

    Quantum motion of a charged particle in a magnetic field

    Once I know the Hamiltonian, I know to take the determinant ##\left| \vec H-\lambda \vec I \right| = 0 ## and solve for ##\lambda## which are the eigenvalues/eigenenergies. My problem is, I'm unsure how to formulate the Hamiltonian. Is my potential ##U(r)## my scalar field ##\phi##? I've seen...
  36. Achintya

    What is the reality of the Electric Force & Field?

    Please help. Thank you.
  37. hugo_faurand

    I Find Einstein's Field Equation - Intuition with Strong Equivalence Principle

    Hello everyone ! I'm getting into General relativity. I wonder know how we find the Einstein's field equation. Maybe we can have an intuition with the strong equivalence principle. So if you can enlight me ☺️☺️ please Regards
  38. eedftt

    Mastering Physics Homework about Magnetic field

    Magnetic fields are sometimes measured by balancing magnetic forces against known mechanical forces. Your task is to measure the strength of a horizontal magnetic field using a 12-cm-long rigid metal rod that hangs from two nonmagnetic springs, one at each end, with spring constants 1.3 N/m ...
  39. G

    Line integral where a vector field is given in cylindrical coordinates

    What I've done so far: From the problem we know that the curve c is a half-circle with radius 1 with its center at (x,y) = (0, 1). We can rewrite x = r cos t and y = 1 + r sin t, where r = 1 and 0<t<pi. z stays the same, so z=z. We can then write l(t) = [x(t), y(t), z ] and solve for dl/dt...
  40. W

    Why a steel plate can shield magnetic field?

    If I put a very long steel plate above a coil with DC, the magnetic field above the plate will decrease because of the shielding of the steel plate. However, from the perspective of magnetci domain, some domains will be magnetized to turn to the direction of the magnetic field from the coil...
  41. F

    I Electromagnetic field according to relativity

    Hello, I am still trying to fully grasp the general idea of the EM field, which always travels at the speed of light regardless of the reference frame, and is represented by a tensor with 16 components in relativity theory. My understanding is that, depending on the observer's frame of...
  42. K

    Clarification on field intensity (electromagnetism)

    Is the intensity of a general electromagnetic wave always the norm of its Poyinting vector? Or are there other notions of intensity?
  43. B

    Electric Force and Field homework problem

    This is my homework. And we don't have online lessons. But my teacher gave this for homework. I couldn't solve this problem. Can you help me?
  44. John Greger

    A Solving Problems in "Conformal Field Theories" by Francesco

    I have been following the book called "Conformal Field Theories" by Francesco, also known as "the yellow pages". I do this for fun but, of course, sometimes it gets rather technical. Do there exist solutions to the problems in this book? I haven't found a solutions manual available. Many...
  45. Rongeet Banerjee

    Work, Energy and Power for a Particle moving in a Potential Field

    But yet again my text says that option 4 is correct.
  46. Seyit KAPLAN

    How is the thermal conductivity affected by magnetic field?

    Hello, I'm searching for how magnetic field affects the thermal conductivity of the metal (such as steel in solid form). If someone suggests any article about it will be very helpful.
  47. P

    Electric field in the Spherical Cavity

    a. For the question a the solution is If the uniform charge density is ρ then the charge of the sphere up to radius r is q = ρ * (4/3)*π * r3; Hence the electric field is E = (ρ *4π*r^3)/(3*εο*r^2); E = (ρ*r)/(3εο); b. I don't understand what is superposition? How to proceed? Please advise.
  48. Bilbo B

    Magnetic field affecting a circular loop

    If the magnetic field is constant then no change in flux will bring no induced emf nor any induced current. With the loop is in rest position the external magnetic field will exert a force but to calculate that force with the help of magnetic field isn't obvious. If this were a charged loop, the...
  49. D

    Thick square loop made of Al with the top half exposed to a B field

  50. F

    Proving Existence of b in F for Field with Char p and Reducible f

    Suppose ##f## is reducible over ##F##. Then there exists ##g, h \in F## such that ##g, h## are not units and ##f = gh##. If there exists ##b \in F## such that ##b^p = a##, then ##(x - b)^p = x^p - b^p = x^p - a##, using the fact that ##F## has characteristic ##p##. So, if such a ##b \in F##...
Back
Top