Why can "dx" in integration be multiplied?

[Kelly333]

Hi,
This is an example in "Barron AP calculus"

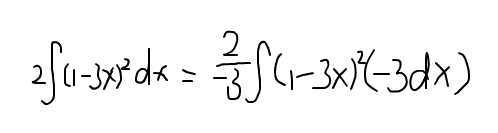
I learned from some past threads that "dx" in integration either means △x which is a infinite number or indicates the variable with respect to which you're integrating.
In the equation above, it seems that dx is multiplied by (1-3x)^2. Isn't dx just a notation?

I haven't learned definate integrals so far so please explain in detail if your answer is related to that.

Thanks.

 

[cnh1995]

△x which is a infinite number

I don't understand what you mean here by infinite number. It is an infinitesimally small change in x. If you refer definite integration expressed as a limit of sum, you'll see that dx is actually the infinitesimal width of the rectangular strip(area element) and y is the height of of the strip. Hence, it's area becomes y*dx and when you sum the areas of all such strips having width dx and height y over an interval, you get the total area under the curve. This sum is nothing but integration of y w.r.t x in that interval i.e.∫y⋅dx.

 

[HallsofIvy]

In this problem, "dx" is simply a symbol telling us which variable this is to be integrated with respect to. It never "means [itex]\Delta x[/itex] which is a infinite number"- I don't know where you got that! But it is not "multiplied by (1- 3x)^2". The notation here is just asking you to integrate the function [itex]2(1- 3x)^2[/itex] with respect to x.

 

[Kelly333]

In this problem, "dx" is simply a symbol telling us which variable this is to be integrated with respect to. It never "means [itex]\Delta x[/itex] which is a infinite number"- I don't know where you got that! But it is not "multiplied by (1- 3x)^2". The notation here is just asking you to integrate the function [itex]2(1- 3x)^2[/itex] with respect to x.

Thanks for your answer! If dx is just a symbol telling us which variable this is to be integrated with respect to, what does (-3*dx) actually means?

 

[Kelly333]

I don't understand what you mean here by infinite number. It is an infinitesimally small change in x. If you refer definite integration expressed as a limit of sum, you'll see that dx is actually the infinitesimal width of the rectangular strip(area element) and y is the height of of the strip. Hence, it's area becomes y*dx and when you sum the areas of all such strips having width dx and height y over an interval, you get the total area under the curve. This sum is nothing but integration of y w.r.t x in that interval i.e.∫y⋅dx.

Thanks for correcting that error! But in antidifferentiation, does dx also mean delta x?

 

[Ray Vickson]

Thanks for correcting that error! But in antidifferentiation, does dx also mean delta x?

No. Typically, we use the notation ##\Delta x## when writing finite sums such as ##\sum_{i=1}^n f(x_i) \Delta x_i##, and ##dx## in the limit as we take ##n \to \infty## and each ##\Delta x_i \to 0##. Of course, "##dx##" is just notation; it is not really "zero".

Now let's look in more detail at your little example. First, do you agree that initially we want to integrate ##(1-3x)^2## with respect to ##x##? We can indicate this fact by introducing the ##dx## notation, but that is not really necessary. In some computer-algebra systems we drop the ##dx## altogether; for example, in Maple we can write "int((1-3*x)^2,x)" to indicate the integrand (before the ",") and the integration variable (after the ","). In Wolfram Alpha you can just enter "integrate (1-3*x)^2 with respect to x".

Anyway, we want to change variables to ##y = 3x##, so the integrand involves the simpler-looking expression ##(1-y^2)##. However, if we write ##I_1 = \text{x-integral}\; (1-3x)^2## and ##I_2 = \text{y-integral}\; (1-y)^2##, we DO NOT have ##I_1 = I_2##; in fact, we have ##I_1 = \frac{1}{3} I_2##. Understanding this last equality is where the ##dx, dy## notation becomes helpful: if ##y = 3 x## then ##dy = 3 dx## and so ##dx = \frac{1}{3} dy##. Now when we erase the ##dx## and ##dy## we are still left with the factor 1/3.

 

[Ssnow]

No, ##\Delta x## is not ##d\,x##.

 

[Kelly333]

No. Typically, we use the notation ##\Delta x## when writing finite sums such as ##\sum_{i=1}^n f(x_i) \Delta x_i##, and ##dx## in the limit as we take ##n \to \infty## and each ##\Delta x_i \to 0##. Of course, "##dx##" is just notation; it is not really "zero".

Now let's look in more detail at your little example. First, do you agree that initially we want to integrate ##(1-3x)^2## with respect to ##x##? We can indicate this fact by introducing the ##dx## notation, but that is not really necessary. In some computer-algebra systems we drop the ##dx## altogether; for example, in Maple we can write "int((1-3*x)^2,x)" to indicate the integrand (before the ",") and the integration variable (after the ","). In Wolfram Alpha you can just enter "integrate (1-3*x)^2 with respect to x".

Anyway, we want to change variables to ##y = 3x##, so the integrand involves the simpler-looking expression ##(1-y^2)##. However, if we write ##I_1 = \text{x-integral}\; (1-3x)^2## and ##I_2 = \text{y-integral}\; (1-y)^2##, we DO NOT have ##I_1 = I_2##; in fact, we have ##I_1 = \frac{1}{3} I_2##. Understanding this last equality is where the ##dx, dy## notation becomes helpful: if ##y = 3 x## then ##dy = 3 dx## and so ##dx = \frac{1}{3} dy##. Now when we erase the ##dx## and ##dy## we are still left with the factor 1/3.

Thanks!Your points are clear and easy to understand. Now I grasp the idea that dx is just a symbol but is also crucial in some equations.
But I don't believe it makes sense to multiply dx by (-3) in this equation in my example. Can you explain that?

 

[HallsofIvy]

Thanks for your answer! If dx is just a symbol telling us which variable this is to be integrated with respect to, what does (-3*dx) actually means?

By itself it doesn't mean anything! With an [itex]\int[/itex], [itex]\int -3dx[/itex] it would mean "integrate -3 x". Or, it could be a "differential". "dy= -3 dx" means that however x increases, y will decrease by three times that much. You should never see something like "f(x)dx" by itself. It should either be inside an integral, as [itex]\int f(x) dx[/itex], or in connection with some other differential, as [itex]dy= f(x)dx[/itex].

 

[Ray Vickson]

Thanks!Your points are clear and easy to understand. Now I grasp the idea that dx is just a symbol but is also crucial in some equations.
But I don't believe it makes sense to multiply dx by (-3) in this equation in my example. Can you explain that?

If you change variables to ##y = 3x## you get ## \frac{1}{3} \int (1-y)^2 \; dy##, but if you change to ##y = -3x## you get ##-\frac{1}{3} \int (1+y)^2 \, dy##.

You say " I don't believe it makes sense to multiply dx by (-3) in this equation in my example". Belief has nothing to do with it; there are standard change-of-variable formulas for integration, and they give you the 1/3 or -1/3 factor. What I mean is this: if we want to evaluate
[tex] I = \text{x-integral} \; f(x) [/tex]
we may find it easier to change variables from ##x## to ##y##, where ##x = g(y)##, so that in the integral we will have ##h(y) = f(g(y))## instead of ##f(x)##. However, that is not the end of the story: we also need to "transform the ##dx##", giving
[tex] I = \text{y-integral} \; h(y) g'(y) [/tex]
This is a provable theorem, not something subject to belief or dis-belief.