Why am I getting this weird equation between angle and time?

[Amit1011]

Homework Statement

A particle slides on the surface of a fixed smooth sphere starting from the topmost point. Find the relation between the angle rotated by the particle as it slides down the particle.

Relevant Equations

I tried solving it using energy conservation.

I tried solving this, the equation coming up is given by: θ≈4 cot^(-1)(e^(-3.1305 sqrt(1/R) t)). However, this is not correct as can be seen when plotted: enter image description here

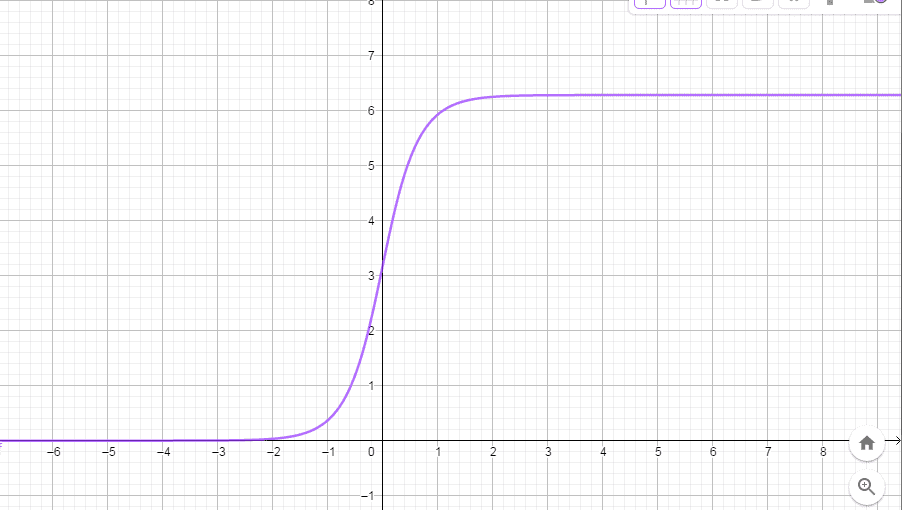
Can somebody please let me know, why is this equation not valid.?

 

[PeroK]

What exactly are you trying to do here? Plot angle against time? If so, what about ##\theta(t) = 0## (for all ##t##)?

 

[Amit1011]

Yes, I'm trying to plot theta vs. t

I can understand, why you would think that theta =0 for all values of t. But considering that the surface of the sphere is smooth, even slightest disturbance from its unstable equilibrium position will cause it to start sliding over the surface of the sphere. This question is about that. At theta = Cos^(-1)(2/3), it will fly off from the surface of the sphere. But until that happens, what will be the relation between theta and time ?

 

[PeroK]

Yes, I'm trying to plot theta vs. t

I can understand, why you would think that theta =0 for all values of t. But considering that the surface of the sphere is smooth, even slightest disturbance from its unstable equilibrium position will cause it to start sliding over the surface of the sphere. This question is about that.

The particle might take some time to get started!

 

[Vanadium 50]

Please include a) the complete and correct problems statement and b) your work in solving it.

 

[etotheipi]

I am also a little confused. @PeroK is right, the problem statement as you have written suggests that the particle will remain at rest on the top of the sphere indefinitely.

In the case that you give it a slight disturbance, i.e. maybe you start the particle from rest at ##\theta = \varepsilon## where ##\varepsilon## is pretty close to ##0##. If you want to do it by energy, then during the interval in which the particle is in contact with the sphere, you would get something like$$mgR(1-\cos{\theta}) = \frac{1}{2}mR^2 \dot{\theta}^2$$ $$\frac{2g}{R}(1-\cos{\theta}) = \dot{\theta}^2$$ $$\int_0^T \sqrt{\frac{2g}{R}} dt = \int_{\varepsilon}^{\theta} \frac{d\theta'}{\sqrt{1-\cos{\theta'}}}$$Just because I've been waiting to use this fancy word for a while, we might say we've reduced the problem to quadratures...

 

[Amit1011]

I started by using this equation (by energy conservation): v^2 = 2gR(1-cos(theta)), where R is the radius of the sphere, and g = 9.8 m/sec^2.

Next equation I used is dv/dt =gSin(theta).

Solving both these equation gave this formula: θ≈4 cot^(-1)(e^(-3.1305 sqrt(1/R) t))

When I plotted, it, It seemed wrong.

I'm just trying to understand, what will be the correct relationship between theta and time.

 

[PeroK]

I'm just trying to understand, what will be the correct relationship between theta and time.

Why do you think there is a relationship between ##\theta## and time?

 

[Amit1011]

Will the particle not fly off from the surface of the sphere, were it to slide down under influence of gravity ? It will fly off when theta = Cos^(-1) (2/3), i.e. at about 48 degrees. But until that happens, theta will vary wrt time.

 

[PeroK]

Will the particle not fly off from the surface of the sphere, were it to slide down under influence of gravity ? It will fly off when theta = Cos^(-1) (2/3), i.e. at about 48 degrees. But until that happens, the theta will vary wrt time.

Maybe ##\theta(t)## depends on ##\theta(t = 0)##?

 

[Amit1011]

Well, that much is clear. Suppose, at t=0, theta is infinitesimally close to zero. Starting with this assumption, what will be the equation between theta and time.?

 

[PeroK]

Well, that much is clear. Suppose, at t=0, theta is infinitesimally close to zero. Starting with this assumption, what will be the equation between theta and time.?

Is that a valid assumption? ##\theta(0) = ?##. What is an "infinitesimal" angle? It's not a number that you can put into the bounds of a definite integral, say.

 

[etotheipi]

Next equation I used is dv/dt =gSin(theta).

Also, why do you need two equations? You could try and solve ##g\sin{\theta} = R\ddot{\theta}##

 

[PeroK]

Is that a valid assumption? ##\theta(0) = ?##. What is an "infinitesimal" angle? It's not a number that you can put into the bounds of a definite integral, say.

PS why not try ##\theta(0) = \theta_0##, where ##\theta_0## is some small finite angle?

 

[Amit1011]

PS why not try ##\theta(0) = \theta_0##, where ##\theta_0## is some small finite angle?

That is the assumption I'm also using, but limiting it to theta_0 tends to zero

 

[PeroK]

That is the assumption I'm also using, but limiting it to theta_0 tends to zero

What happens when you let ##\theta_0 \rightarrow 0##?

 

[Amit1011]

when theta_0 tends to 0, but is not exactly equal to 0, it will definitely start to slide down the surface of the sphere. It will continue to be on the surface of the sphere until theta = 48.18 degrees(approx). It will then fly off in parabolic path. I'm trying to find the equation between theta and time t, until the particle flies off the surface of the sphere.

 

[PeroK]

when theta_0 tends to 0, but is not exactly equal to 0, it will definitely start to slide down the surface of the sphere. It will continue to be on the surface of the sphere until theta = 48.18 degrees(approx). It will then fly off in parabolic path. I'm trying to find the equation between theta and time t, until the particle flies off the surface of the sphere.

Okay. Suppose we calculate ##T(\theta_0)##, which is the total time it takes from starting near the top of the sphere (at rest from an initial angle ##\theta_0)## until it flies off. Maybe ##T(\theta_0) \rightarrow \infty## as ##\theta_0 \rightarrow 0##?

 

[Amit1011]

Also, why do you need two equations? You could try and solve ##g\sin{\theta} = R\ddot{\theta}##

It's an

Is there any software where I could plot it.? I don't know how to solve this differential equation.

 

[PeroK]

It's an View attachment 268186
Is there any software where I could plot it.? I don't know how to solve this differential equation.

I think you are struggling with the concept of a problem that does not have a solution! You can solve this for any non-zero ##\theta_0##, but it's not valid to take ##\theta_0 = 0## or the limit as ##\theta_0 \rightarrow 0##.

 

[Vanadium 50]

Can we please stop until a) the OP gives us the complete and correct problem statement and b) his complete attempt at a solution?

Or, alternatively, can we solve it for him so he can put a box around it and call it his own work?

 

[etotheipi]

It's an View attachment 268186
Is there any software where I could plot it.? I don't know how to solve this differential equation.

Here's something you could try...$$g\sin{\theta} = R\frac{d^2 \theta}{dt^2}$$Now let's introduce a change of variables ##u = \frac{d\theta}{dt}##, so that$$\frac{d^2 \theta}{dt^2} = \frac{du}{dt} = \frac{du}{d\theta} \frac{d\theta}{dt} = u\frac{du}{d\theta}$$So the differential equation is now$$g\sin{\theta} = Ru\frac{du}{d\theta}$$That is separable, so integrate and you'll find$$u^2 = \frac{2g}{R}(1-\cos{\theta}) \implies \frac{d\theta}{dt} = \sqrt{\frac{2g}{R}} \sqrt{1-\cos{\theta}}$$Hopefully you will notice that this is exactly the same differential equation that was obtained by considering energy, back in #6!

 

[Amit1011]

Here's something you could try...$$g\sin{\theta} = R\frac{d^2 \theta}{dt^2}$$Now let's introduce a change of variables ##u = \frac{d\theta}{dt}##, so that$$\frac{d^2 \theta}{dt^2} = \frac{du}{dt} = \frac{du}{d\theta} \frac{d\theta}{dt} = u\frac{du}{d\theta}$$So the differential equation is now$$g\sin{\theta} = Ru\frac{du}{d\theta}$$That is separable, so integrate and you'll find$$u^2 = \frac{2g}{R}(1-\cos{\theta}) \implies \frac{d\theta}{dt} = \sqrt{\frac{2g}{R}} \sqrt{1-\cos{\theta}}$$Hopefully you will notice that this is exactly the same differential equation that was obtained by considering energy, back in #6!

This is exactly the differential equation that I figured out while I was attempting to solve it. On solving this equation, the equation I got was θ≈4 cot^(-1)(e^(-3.1305 sqrt(1/R) t)) , which I've posted in my original post. By plotting it in a mathematical software(Geogebra), what I saw, I've posted that too in my original post. But, the plot is not showing the behaviour that I was expecting. For eg, the graph crosses y axis(which is theta) at 3.14 radians, and becomes flat after a while. But the graph should have crossed at the origin. That would have made sense. That's why I asked in my original post, why the equation does not seem valid. I even considered that exactly t=0 (x axis being t), the equation will not be valid, but at every other point in time, it should be valid, but the graph becomes flat after a while, but the value at which the graph becomes almost flat makes no sense either(even after converting in degrees).

 

[etotheipi]

How did you solve it, did you do it numerically? Which angle did you use as your ##\theta_0## in the definite integral; as you are probably now aware from the discussion above, ##\theta_0 = 0## won't work.

 

[Amit1011]

I was already aware when I was attempting it by myself, that at theta exactly =0, the equation will not not be solvable, because the particle will be in equilibrium, though unstable equilibrium. However, I used Wolfram alpha, to solve it. It gave the equation that I used to plot the graph.

 

[etotheipi]

I was already aware when I was attempting it by myself, that at theta exactly =0, the equation will not not be solvable, because the particle will be in equilibrium, though unstable equilibrium.

And more alarmingly, the integrand diverges! So, what ##\theta_0## did you use?

 

[kuruman]

Just to put the discussion back on track.

@Amit1011 you can solve the equation posted on #22 by @etothepi using the identity ##1-\cos\theta=2\sin^2(\frac{\theta}{2}).## That eliminates the radical. You will need a ##\theta_0## as the lower limit of the integral which you should be able to do. When I did all this, I was able to get ##\theta(t)## in closed form and plot it. You can get help to arrive at the equation that I got (it doesn't look like the one you posted in #1) and, if you post all your work, we can help pinpoint any errors that may have made. If you don't post your work, it will be difficult for us to help. It is also difficult for us to help you if you post a hybrid form of symbols and numbers such as "θ≈4 cot^(-1)(e^(-3.1305 sqrt(1/R) t))" If you put your equation in symbolic form, I will better be able to compare it with my equation which is also in symbolic form. It took me

Shown below is angle vs. time for three values of ##\theta_0##, 10^-3 (green), 10^-4 (brown) and 10^-5 (blue). The gridline is at the angle where the mass sliedes off. You can see the trend as ##\theta_0## becomes smaller and why it is necessary to have a small but non-zero value for it. Note that 10^-5 rad is quite small, the angle subtended by a meter stick 100 km away.