What must be the (shortest) length of Y in terms of X?

[DaveC426913]

I am 99.5% sure I've got it right, but I keep second-guessing myself.

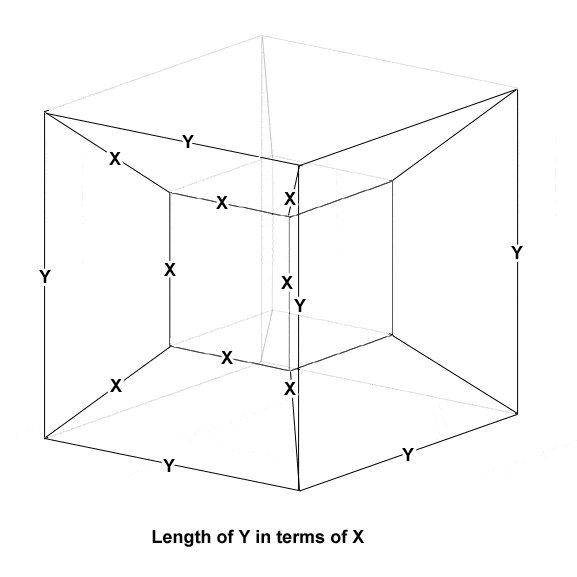
1] Cube with sides of length X.
2] Diagonals out from each corner of length no less than X...
3] ...to an outer cube of sides of length Y.
What must be the (shortest) length of Y in terms of X?

I get [tex] y = 2\sqrt{2}x[/tex]

 

[chiro]

Hey DaveC426913.

This is my reasoning for the calculation.

The inner cube's centre is also aligned with the outer cube's centre due to symmetry arguments. Because of the symmetry of the cube the length of the line segment from the centre of the cube to any diagonal is given by pythagoras' theorem and is given by SQRT([1/2X]^2 + [1/2X]^2 + [1/2X]^2) = SQRT(3/4X^2) = SQRT(3/4)X.

Doing the same thing for the outer-cube we get the diagonal from the centre of the cube to the outer vertex to be:

SQRT([1/2Y]^2 + [1/2Y]^2 + [1/2Y]^2) = SQRT(3/4Y^2) = SQRT(3/4)Y

Now we use vector addition in terms of the lengths in that if we start at the centre of the X cube, go to a vertex and then add X to to get to the corresponding vertex for the Y cube, then the length will be the same as the length of diagonal from the centre to the final Y vertex.

This means SQRT(3/4)X + X = SQRT(3/4)Y which implies

SQRT(4/4)X + SQRT(3/4)X = SQRT(3/4)Y
SQRT(7/4)X = SQRT(3/4)Y
Y = SQRT(7/3)X

which is different to what you got.

Again, the assumptions I made are as follows:

1) Both cubes have a centroid at the same point to due to symmetry (main assumption)
2) Both cubes have a semi-diagonal starting from the centre and finishing at a vertex for a cube given with an edge length of C to be given by SQRT((C/2)^ + (C/2)^2 + (C/2)^2) = SQRT(3/4)C\
3) The ray segment of the semi-diagonal for the outer cube through vector addition has the length of the inner semi-diagonal plus the length of the inner cube edge (as given by your picture).
4) Solving these two gives one cube edge in terms of another.

 

[haruspex]

SQRT(3/4)X + X = SQRT(3/4)Y

I agree up to there, but then I think you went wrong.
The above gives Y = X(1 + 2√3/3)

 

[chiro]

I agree up to there, but then I think you went wrong.
The above gives Y = X(1 + 2√3/3)

Yeah that was a bad error :). Should have been (SQRT(3) + 2)/SQRT(3)!

 

[AlephZero]

The diagonal of a cube with side ##a## is ##\sqrt 3 a## (use Pythagoras' theorem twice, to find the diagonal of a face and then the diagonal of the cube)

So measuring the diagonals of the outer cube two different ways, ##\sqrt 3 y = \sqrt 3 x + 2x##.

 

[DaveC426913]

The fact that y'all got different results leads me to wonder if I'm undertthinking it. My thinking is as follows.

The 3Dness of the geometry is a red herring. It simply comes down to the trapezoid YXXX.

Y will equal X plus the side-length of two right triangles whose hypotenuse is X.

 

[AlephZero]

The 3Dness of the geometry is a red herring. It simply comes down to the trapezoid YXXX.

Yes, but ...

Y will equal X plus the side-length of two right triangles whose hypotenuse is X.

... that doesn't give you an answer, unless you know the angles in the trapezoid. At the ridiculous extremes, you could draw it with X = Y (a square, with the center of the cube an infinite distance away), or with X = Y/3 (squashed completely flat).

You must have assumed something wrong about the angles, to get the wrong answer in your OP.

Actually, we didn't all get different answers - mine was just a quicker way to get the same as Chiro's final version.

 

[DaveC426913]

You must have assumed something wrong about the angles, to get the wrong answer in your

Why would they not be 45 degrees?

 

[skiller]

Why would they not be 45 degrees?

Consider the triangle defined by the following points:

A) one of the vertices of the inner cube;
B) the mid-point of one of the three edges of the inner cube which have an end-point coinciding with the above vertex;
C) the centre of the inner cube.

Can you see that the angle that you are assuming to be 45° is actually the angle ACB ?

Using this example, it looks like you are assuming that AB = X/2 (correct) and that BC = X/2 also (wrong).

 

[AlephZero]

Why would they not be 45 degrees?

You can make a scale drawing if you don't like the math. Imagine you slice the cube across the diagonal of two opposite faces. The cut surface is a rectangle with two sides length y (two edges of the origianal cube) and the other two ##\sqrt 2 y## (the diagonals of the cube faces).

Two of your trapezia lie in that plane. The "sloping" sides are parts of the diagonals of the rectangle. The angle between them is about 35 degrees not 45.

 

[chiro]

The fact that y'all got different results leads me to wonder if I'm undertthinking it.

All of the responses got the same final results, but my initial final answer was wrong due to mistakes in arithmetic.

Did you read my response regarding the derivation?

 

[skiller]

Also, am I the only one wondering what the BIB in the following means?

2] Diagonals out from each corner of length no less than X...

What must be the (shortest) length of Y in terms of X?

Your diagram suggests that it extends by exactly X.

And Y can be calculated precisely in terms of X, no matter how much the diagonal extends - there is no concept of "shortest" in this situation really, is there?

 

[DaveC426913]

You can make a scale drawing if you don't like the math. Imagine you slice the cube across the diagonal of two opposite faces. The cut surface is a rectangle with two sides length y (two edges of the origianal cube) and the other two ##\sqrt 2 y## (the diagonals of the cube faces).

Two of your trapezia lie in that plane. The "sloping" sides are parts of the diagonals of the rectangle. The angle between them is about 35 degrees not 45.

Yeah. I see my assumption that the trapezoid has 45 degree angles was simplistic. Just after I posted I started drawing a cross section of the cube through its diagonal and I see it's a squat rectangle. Thus its diagonals are certainly not 45 degrees.

 

[DaveC426913]

The fact that y'all got different results leads me to wonder if I'm undertthinking it.

Yes, but ...

Actually, we didn't all get different answers

I'm sorry, that came out wrong. I didn't mean from each other; I meant y'all got different answers from me. Which led me to question my own.

 

[DaveC426913]

I agree up to there, but then I think you went wrong.
The above gives Y = X(1 + 2√3/3)

This gives me Y=~1.96X.

 

[DaveC426913]

Also, am I the only one wondering what the BIB in the following means?Your diagram suggests that it extends by exactly X.

And Y can be calculated precisely in terms of X, no matter how much the diagonal extends - there is no concept of "shortest" in this situation really, is there?

This is where it gets tricky.

This is a physical object. The entire device is made of 32 identical telescoping rods. X and Y are the same rod. Because they can telescope, the diagonals can stretch. The shape is not rigid. The outer cube could expand and distort without the inner cube expanding.

All this is incidental to you. The point is that what I am ultimately attempting to do is calculate by how much the rod must be able to telescope to be both X and Y. If the rods were designed such that they could expand arbitrarily long, then the cubes could expand and/or distort arbitrarily. But to make the shape in the diagram, there is a minimum amount.

 

[haruspex]

This gives me Y=~1.96X.

No, more like 2.15X.

 

[DaveC426913]

No, more like 2.15X.

Ah. Right. It's root 3. I did cube root.That's excellent. That means all my work to make 3X telescoping rods is not necessary.

 

[DaveC426913]

OK, I've built a static prototype out of wooden skewers and hot glue.

With X=2.2" in my prototype, I measure Y= at 4.7". That's accounting for the non-zero diameter of the sticks.

So my empirical ratio is 2.14.

haruspex wins! (And honourable mention to chiro for his derivation.)And that means that the device can be constructed using 24 identical rods that can telescope by a factor of at least 2.15. That's way better than the 3+ I had originally calculated! (Do you know how difficult it is to construct a rod that can telescope to 3x its own length?)