What is the Lagrangian, equations of motion for this system?

[Amitayas Banerjee]

<<Moderator's note: Moved from a technical forum, no template.>>

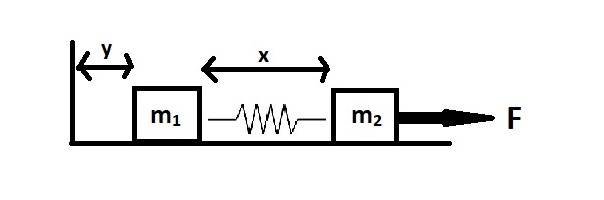
Description of the system:
The masses m₁ and m₂ lie on a smooth surface. The masses are attached with a spring of non stretched length l₀ and spring constant k. A constant force F is being applied to m₂.

My coordinates:
Left of m₁ there is a stationary wall. The distance between m₁'s left surface and the wall is represented as y and the distance between the right and left surfaces of m₁ and m₂, respectively, is represented as x.

What my brain says:
The kinetic energy of this system is equal to the sum of kinetic energies of the two masses, i.e,
$$\frac{1}{2}m_1 \dot{y}^2 + \frac{1}{2}m_2 (\dot{x}+\dot{y})^2$$
and the potential energy is just the spring potential, i.e,
$$\frac{1}{2} k (x-l_0)^2$$
Therefore, the Lagrangian seems to be,
$$L=\frac{1}{2}m_1 \dot{y}^2 + \frac{1}{2}m_2 (\dot{x}+\dot{y})^2 - \frac{1}{2} k (x-l_0)^2$$

Now, the generalized force is
$$F\cdot \frac{\partial {(x+y)}}{\partial x}$$
So, the equations of motion seem to be,
$$\frac{d}{dt}(\frac{\partial L}{\partial {\dot x}}) - \frac{\partial L}{\partial { x}}=F$$
and
$$\frac{d}{dt}(\frac{\partial L}{\partial {\dot y}}) - \frac{\partial L}{\partial { y}}=0$$Is this correct? Or am I missing something? Please help me figure out the mistakes.

 

[Orodruin]

Your coordinates are set up in such a manner that the displacement depends on both x and y.

Also note that you perfectly well can treat the force using a potential, since it is conservative.

 

[Amitayas Banerjee]

Your coordinates are set up in such a manner that the displacement depends on both x and y.

Sir, What is the problem if the displacement of m₂ depends on both x and y? How can I modify my equations for that? Is there any problem with my generalized force calculation?

 

[Orodruin]

The generalised force for any coordinate is given by ##F(\partial \ell/dq^i)##, where ##\ell## is the displacement and ##F## the force. You have ignored the effect of the generalised force on the ##y## coordinate.

 

[Amitayas Banerjee]

You have ignored the effect of the generalised force on the yyy coordinate.

Is it not $$F\cdot \frac{\partial {(x+y)}}{\partial x}$$
The factor of F becomes 1. Does it not?

 

[Orodruin]

Is it not $$F\cdot \frac{\partial {(x+y)}}{\partial x}$$
The factor of F becomes 1. Does it not?

That is just the effect on the ##x## coordinate, but you are ignoring the fact that ##x + y## also depends on ##y##.

 

[Amitayas Banerjee]

That is just the effect on the xxx coordinate, but you are ignoring the fact that x+yx+yx + y also depends on yyy.

Then my second equation of motion is $$
\frac{d}{dt}(\frac{\partial L}{\partial {\dot y}}) - \frac{\partial L}{\partial { y}}=F\cdot \frac{\partial {(x+y)}}{\partial y}$$? Is it correct now?

 

[Orodruin]

Yes. However, as I said, it is easier to do this by including a potential in the Lagrangian.

 

[Amitayas Banerjee]

Sir, what are the finally correct equations? Are they
$$\frac{d}{dt}(\frac{\partial L}{\partial {\dot x}}) - \frac{\partial L}{\partial { x}}=F$$

and

$$\frac{d}{dt}(\frac{\partial L}{\partial {\dot y}}) - \frac{\partial L}{\partial { y}}=F$$
? Please clarify this

 

[Delta2]

I think they are correct now, probably Orodruin wants to incorporate the external force into the Lagrangian by adding a term -F(x+y) as extra potential energy to the lagrangian, so it will be ##L'=L-F(x+y)## and the equations of motion with ##L'## will be homogeneous.