What if n is in the summation?

[mohabitar]

I'm trying to get a closed form of a summation, however n is in the summation itself. Here's an example:

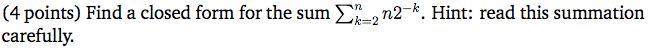
Ive never encountered such a thing. What happens to the n? Does it stay in there as n in the closed form? So then we have n/2^k which the closed form turns out to be:

n/ [2^(n+1)-1 / (2-1)]

However, when I tested my solution using a test value, the two versions didnt check out, so obviously I'm doing something wrong. And the instructions say to read the question carefully, which is kinda scary as wel.

 

[rock.freak667]

I don't think 'n' depends on 'k', so you can effectively treat it as a constant and factor it out of the summation.

 

[mohabitar]

So then were left with 1/2^k. However, if we use this formula for .5^k, we get [.5^(n+1)-1 / (.5-1)] multiplied by the N we factored out, and when we use a test value of say n=3, the manual summation and the closed form total do not equal, meaning there had to be some mistake.

 

[rock.freak667]

So then were left with 1/2^k. However, if we use this formula for .5^k, we get [.5^(n+1)-1 / (.5-1)] multiplied by the N we factored out, and when we use a test value of say n=3, the manual summation and the closed form total do not equal, meaning there had to be some mistake.

Are you sure what you posted is the correct solution?

Also, in your formula are you accounting for the fact that your sum starts at k=2 and not k=1 or 0 ?

 

[mohabitar]

Yes I'm sure. Here's my work:

Sorry its a little big, here's the direct link for smaller viewing: http://i.imgur.com/UJqVh.jpg

 

[vela]

You need to think about this question rock.freak asked:

Also, in your formula are you accounting for the fact that your sum starts at k=2 and not k=1 or 0 ?

 

[epenguin]

The purpose of this exercise was to make sure you read such expressions properly, not taking it for something else that looks vaguely the same. For comment of yours this looks to have been necessary and useful. As this is the main point, for the actual series they gave you something easy. However you are making a bit heavy weather of it, though I expect you have seen geometrical series before now.


You take out the factor n. Now I will talk about the rest but don't forget to but the n back at the end.

One way to do it is to write,

[tex] \sum_{k=2}^n 2^{-k} = 2^{-2} + 2^{-3} + ... + 2^{-n}[/tex]

[tex] = \sum_{k=2}^\infty 2^{-k} - \sum_{k=n+1}^{\infty} 2^-^k[/tex]

Now can you see the second infinite sum here is the same as the first multiplied by a factor? (If you can't yet see this, then write this series out explicitly like I have in the top line).I would take out this factor, then you will see you can write the thing as product of a finite expression multiplying the well-known infinite series (which is actually a bit easier to sum than a finite one! and anyway you seem to know it). If you do these steps of make progress on the problem the way you were doing but get it right via the hints I will show you something nice about the infinite series.

Actually now I have looked at your calc. again you could use the same idea of a factor in the calculation you have done (you are applying a formula from a book or somewhere without looking carefully what exactly it is a formula for.)

Could you now take away your big image since it makes the page awkward to use.