What are the non-zero Christoffel symbols for 2D polar coordinates?

[flaticus]

Just started self teaching myself differential geometry and tried to find the christoffel symbols of the second kind for 2d polar coordinates. I am checking to see if I did everything correctly.

With a line element of:

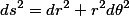therefore the metric should be:

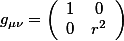The christoffel symbols of the second kind can be found by:

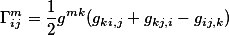And the non-zero christoffel symbols I found:

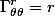
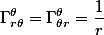
I noticed since

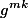is symmetric it is non-zero when m=k so summing over k is not needed, i do not know if I missed anything by doing this.

 

[PeterDonis]

i do not know if I missed anything by doing this.

You didn't miss any non-zero christoffel symbols, but you need to check the sign of ##\Gamma^r_{\theta \theta}##.

 

[flaticus]

You didn't miss any non-zero christoffel symbols, but you need to check the sign of ##\Gamma^r_{\theta \theta}##.

Ahh, I see was just looking at christoffel equation while doing derivatives in head and forgot to carry the negative. Thank you.

 

[Orodruin]

Just a quick note, there are easier ways of getting the Christoffel symbols than inserting the metric into the expression from the Levi-Civita connection.

 

[PAllen]

Just a quick note, there are easier ways of getting the Christoffel symbols than inserting the metric into the expression from the Levi-Civita connection.

I'm curious - whenever I do one by hand, I do as the OP did. What are these easier ways?

 

[Orodruin]

I'm curious - whenever I do one by hand, I do as the OP did. What are these easier ways?

I would start by deriving the geodesic equations for the metric and identify the Christoffel symbols from there. Perhaps you do not find that simpler?

Edit: In the case of polar coordinates, minimise
$$
S = \int (r^2 \dot \phi^2 + \dot r^2) d\tau
$$
Euler-Lagrange equations give:
\begin{eqnarray}
\ddot r - r \dot\phi^2 &=& 0 \\
\ddot \phi + 2\frac{1}{r} \dot r \dot \phi &=& 0
\end{eqnarray}
Identification with ##\ddot x^\mu + \Gamma^\mu_{\nu\rho} \dot x^\nu \dot x^\rho = 0## along with the zero torsion of the Levi-Civita connection gives
$$
\Gamma^r_{\phi\phi} = - r, \quad \Gamma^\phi_{r\phi} = \Gamma^\phi_{\phi r} = \frac 1r.
$$

 

[HallsofIvy]

Good job! Now, go on to the sphere!

Actually, a bit harder would be for an ellipse or the surface of an ellipsoid.

 

[PAllen]

I would start by deriving the geodesic equations for the metric and identify the Christoffel symbols from there. Perhaps you do not find that simpler?

Edit: In the case of polar coordinates, minimise
$$
S = \int (r^2 \dot \phi^2 + \dot r^2) d\tau
$$
Euler-Lagrange equations give:
\begin{eqnarray}
\ddot r - r \dot\phi^2 &=& 0 \\
\ddot \phi + 2\frac{1}{r} \dot r \dot \phi &=& 0
\end{eqnarray}
Identification with ##\ddot x^\mu + \Gamma^\mu_{\nu\rho} \dot x^\nu \dot x^\rho = 0## along with the zero torsion of the Levi-Civita connection gives
$$
\Gamma^r_{\phi\phi} = - r, \quad \Gamma^\phi_{r\phi} = \Gamma^\phi_{\phi r} = \frac 1r.
$$

No, I just never thought of doing it that way. Since Euler-Lagrange are used to derive the general geodesic equation with Christoffel symbols, it really never occurred to me that for simple metrics their direct application would be simpler than the general definition.

 

[Orodruin]

No, I just never thought of doing it that way. Since Euler-Lagrange are used to derive the general geodesic equation with Christoffel symbols, it really never occurred to me that for simple metrics their direct application would be simpler than the general definition.

To be honest I think it is even more simplifying for worse metrics (in particular off-diagonal ones), where otherwise you would have a large number of terms and partial derivatives of the metric to compute and keep track of. I have not done the counting, but I do believe that this approach significantly reduces the amount of necessary book keeping. Although you will still need to compute the same derivatives, it somehow feels lighter that you do not have to write them down more than once and the book keeping of knowing which derivative goes where is handled automagically.

 

[PAllen]

To be honest I think it is even more simplifying for worse metrics (in particular off-diagonal ones), where otherwise you would have a large number of terms and partial derivatives of the metric to compute and keep track of. I have not done the counting, but I do believe that this approach significantly reduces the amount of necessary book keeping. Although you will still need to compute the same derivatives, it somehow feels lighter that you do not have to write them down more than once and the book keeping of knowing which derivative goes where is handled automagically.

That makes a lot of sense. For transforming the metric from one set of coordinates to another, I basically never use the Jacobian definition; I substitute in the physicists metric short hand. It just never occurred to me that using Euler-Lagrange would avoid lots of bookkeeping for computation of Christoffel symbols. A years PF contribution is now paid for in saved computation.

 

[flaticus]

Good job! Now, go on to the sphere!

Actually, a bit harder would be for an ellipse or the surface of an ellipsoid.

For spherical coordinates this is what I found:
##ds^2 = dr^2 + r^2 d\theta^2 + r^2 sin\theta^2 d\phi^2##

##\Gamma^r_{\theta \theta} = -r \\
\Gamma^r_{\phi \phi} = -rsin^2 \theta \\
\Gamma^\theta_{r \theta} = \Gamma^\theta_{\theta r} = \frac{1}{r} \\
\Gamma^\theta_{\phi \phi} = -sin\theta cos\theta \\
\Gamma^\phi_{r \phi} = \Gamma^\phi_{\phi r} = \frac{1}{r} \\
\Gamma^\phi_{\theta \phi} = \Gamma^\phi_{\phi \theta} = cot\theta ##