Understanding Vector Addition in Physics

[SweatingBear]

I am stuck on this one:

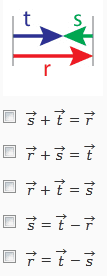
According to me, the only correct answers are

[itex]\vec{r} = \vec{t} - \vec{s} \\ \vec{r} + \vec{s} = \vec{t}[/itex]

But according to the key, these are also correct

[itex]\vec{r} + \vec{t} = \vec{s} \\ \vec{s} + \vec{t} = \vec{r} [/itex]

I honestly do not see how, can somebody please explain?

 

[mfb]

But according to the key, these are also correct

[itex]\vec{r} + \vec{t} = \vec{s} \\ \vec{s} + \vec{t} = \vec{r} [/itex]

Those are wrong, unless you have some special, weird vector spaces.

 

[CompuChip]

However it does look like t - r = s.

 

[mfb]

That is another valid equation. t=r+s, r=t-s and s=t-r are equivalent.

 

[SweatingBear]

Thanks.