- #1
bgq
- 162
- 0
Hi,
How can we explain this paradox:
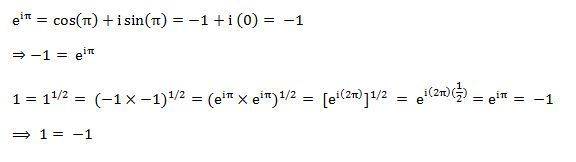
Thanks in advance.
How can we explain this paradox:
Thanks in advance.
That depends upon exactly how you define [itex]a^{1/2}[/itex] (in wikipedia, as the principal root). The way bgq was using it was invalid.rubi said:The illegal step is [itex](e^{i2\pi})^{1/2}=e^{i2\pi \cdot \frac{1}{2}}[/itex]. The step [itex]1=1^{1/2}[/itex] is completely valid (see http://en.wikipedia.org/wiki/Square_root#Principal_square_root_of_a_complex_number).
bgq said:I think 1 = 11/2 is valid because even in complex number system, if we assume 11/2 = a + ib we get a = 1 and b = 0.
HallsofIvy said:For real numbers, "the" square root function of "a" is defined as "the positive number, b, such that [itex]b^2= a[/itex]". For the complex numbers, which do not form an ordered field and so we cannot separate into "positive" and "negative" numbers, we can distinguish so easily between the two square roots and so we cannot say "[itex]1^{1/2}= 1[/itex]". There are two numbers whose square is 1, 1 and -1, and we cannot simply assert that 11/2 is either 1 or -1.
In short, your error is in the first step, asserting that 1= 11/2. That is true as long as you stay in the real numbers. As soon as you extend into the complex numbers, you cannot say that.
rubi said:The illegal step is [itex](e^{i2\pi})^{1/2}=e^{i2\pi \cdot \frac{1}{2}}[/itex]. The step [itex]1=1^{1/2}[/itex] is completely valid (see http://en.wikipedia.org/wiki/Square_root#Principal_square_root_of_a_complex_number).
rubi said:The point I'm trying to make is that the term [itex]1^{1/2}[/itex] is in my opinion generally accepted to be interpreted using principal values,
Interpretation is the wrong word. It is a definition. For two complex numbers [itex]w[/itex] and [itex]z[/itex], we define [itex]w^z[/itex] to be equal to [itex]e^{z\log w}[/itex], where [itex]\log[/itex] is the principal logarithm. This is a completely valid definition that is found in every math text on complex analysis and we can use it to rigorously prove [itex]1^{1/2} = 1[/itex].rbj said:rubi, i don't think that mathematical proofs can be supported by what is generally accepted interpretation.
No. By squaring the equation, you introduced an extra solution that is not a solution to the initial equation. These two equations aren't equivalent. The same thing happens for example when you start with [itex]x=1[/itex]. This obviously has only one solution, which is [itex]1[/itex], but it you square it, you get [itex]x^2 = 1[/itex], which has two solutions [itex]1[/itex] and [itex]-1[/itex]. The same thing also holds for trigonometric functions. [itex]\arcsin(0)[/itex] is defined to be [itex]0[/itex], although [itex]\sin(\pi k)=0[/itex] for every integer [itex]k[/itex].the only valid thing to say (unless one has more information about [itex]x[/itex]) about
[tex] y^{1/2} = x [/tex]
is that
[tex] x^2 = y [/tex]
nothing else.
Not to butt in, but...I'm pretty sure we define complex exponentiation by ##w^z=e^{z\ln{w}}## for any given value of the natural logarithm, not just the principle value.rubi said:Interpretation is the wrong word. It is a definition. For two complex numbers [itex]w[/itex] and [itex]z[/itex], we define [itex]w^z[/itex] to be equal to [itex]e^{z\log w}[/itex], where [itex]\log[/itex] is the principal logarithm. This is a completely valid definition that is found in every math text on complex analysis and we can use it to rigorously prove [itex]1^{1/2} = 1[/itex].
Mandelbroth said:Not to butt in, but...I'm pretty sure we define complex exponentiation by ##w^z=e^{z\ln{w}}## for any given value of the natural logarithm, not just the principle value.
Mandelbroth said:Not to butt in, but...I'm pretty sure we define complex exponentiation by ##w^z=e^{z\ln{w}}## for any given value of the natural logarithm, not just the principle value.
jackmell said:The whole branching thing causes a lot of problems, frustrations, and students get turned away from the subject
rubi said:If a student gets frustrated with the math, the student needs to change; not the math.
That depends on the person. For me, working with single-valued functions is much simpler, because you have standard functions [itex]f:\mathbb C\rightarrow\mathbb C[/itex] instead of [itex]f:\mathcal P(\mathbb C)\rightarrow\mathcal P(\mathbb C)[/itex]. But as I said, it's a matter of taste and you need to know both approaches.jackmell said:Depends on why the student is getting frustrated. I've seen examples of math presented poorly. The type of frustration this leads to can be corrected by changing the way math is presented. The way branch-cuts are currently presented in Complex Analysis today leads to frustration on the part of the student, not because he is thick-headed and cannot absorb the concept, rather the concept is not being introduced in a way conducive to comprehension on an intuitive level.
I don't really see where you need multi-valued functions for this problem. You can just solve the integral using standard integration techniques. It might take some time, but i doubt the problem will be easier with the multi-valued approach. It's just shifted to somewhere else.I can give an example of what I mean at the risk of being criticized for it. This is a thread on the complex logarithm. The concept is not easy to comprehend until Alice helps us with it:
https://www.physicsforums.com/showthread.php?t=702808
The complex number paradox is a mathematical concept that arises from the fact that the square root of a negative number is considered non-real, but when squared, it results in a real number. This paradox creates confusion and challenges in understanding the nature of complex numbers.
Complex numbers are primarily used in mathematics and engineering to solve equations that involve negative numbers. They are also used to represent and analyze electrical circuits, signal processing, and quantum mechanics, among other applications.
The origins of the complex number paradox can be traced back to the ancient Greeks, who believed that all numbers must have a geometric representation. Since complex numbers cannot be represented on a traditional number line, they were deemed as "imaginary." This led to confusion and debates among mathematicians for centuries.
The complex number paradox is solved by accepting complex numbers as a valid mathematical concept and understanding their properties. This includes understanding that the square root of a negative number is not a real number, but rather an imaginary number, and that when squared, it results in a negative real number.
Yes, there are many real-life applications for complex numbers. Some examples include analyzing and designing electrical circuits, modeling and predicting weather patterns, and understanding the behavior of stock markets. Complex numbers also have applications in physics, engineering, and computer science.