The derivation of the volume form in Ricci tensor

[bres gres]

TL;DR Summary

https://www.youtube.com/watch?v=oQZTYt_Pxcc&list=PLJHszsWbB6hpk5h8lSfBkVrpjsqvUGTCx&index=28

i found there is one problem in the derivation of this volume form in 18:10.

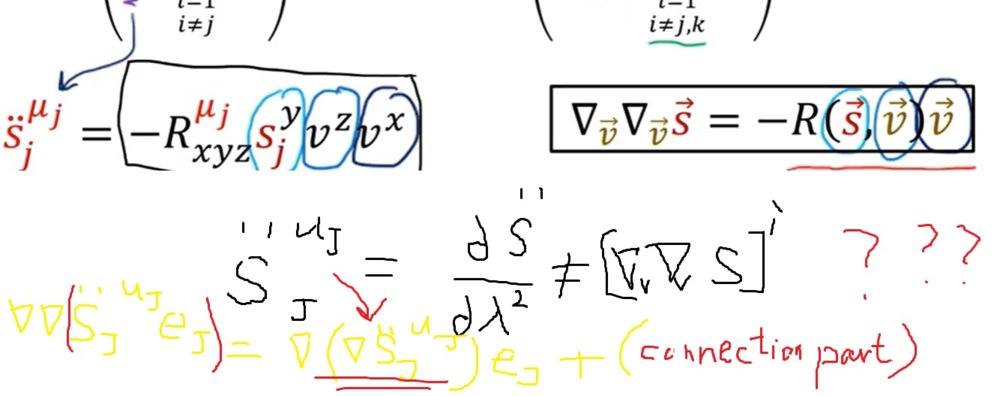
In this derivation,i am not sure why the second derivative of the vector ## S_j '' ## is equal to ## R^{u_j}{}_{xyz} s^y_j v^z y^x##
could anyone explain this bit to me
thank you

it seems ## S_j '' ## is just the "ordinary derivative" part but it is not actually equal to ## R^{u_j}{}_{xyz} s^y_j v^z y^x##

for example: ## d^2(y^i e_i )/dx^2## is not equal to ##d^2(y^i)/dx^2 e^i##
here ## S_j '' ## is just "d(S_j)^2/ dx^2 "" (which is the change of the vector component)without considering the change of the basis vector /connection tensor.
the ##S_j'' ## here is only part of ## R^{u_j}{}_{xyz} s^y_j v^z y^x## ??

The convariant derivative of an input is equal to the normal-type ordinary derivative in scalar function only ,however in the "second covariant derivative" of a vector they are not equal
the scalar s is just the component of the vector s which is the "part of the story"
i can't see why the left side is equal to the right side since they ignore the basis vector
could anyone explain to me
thank you

 

[bres gres]

the problem is : in general,"the second derivative of the [component of vector]" itself(which is the double-dot one) is not equal to the "component of the second derivative of the [whole vector]"(which is the double-Nabla derivative)
therefore i am not sure why they are equal

 

[bres gres]

Due to my unclear expression in the first post,i might post my question again here.Hope everyone can read it clear
sorry about that
In this video,the presenter tried to relate the ordinary derivative of the Volume to the Ricci tensor but i get stuck when i try to understand it.

My problem is i don't understand why ##\ddot{s^{u_j} _j} ##
is equal to ## -R^{\mu_j}{}_{xyz} s^y_j v^z y^x##
in 18:10

The reason is
##\ddot{s^{u_j} _j} ##
should not be equal to
## -R^{\mu_j}{}_{xyz} s^y_j v^z y^x##
where ##[\nabla_v\nabla_vS]^{u^j}= -R^{\mu_j}{}_{xyz} s^y_j v^z y^x ##since they are different things.
The former one is just second ordinary derivative and the latter one is the full-form second covariant derivative.

i cannot see why it is not second ordinary derivative since volume itself a scalar.
if you take derivative of the volume with ordinary derivative,then the logic should follow in a similar manner and the second derivative of the vector component
(part of the decomposition because of product rule) should be the ordinary type derivative

I would now give an example why they are not equal.

Given a 2D-Volume(area) which is spanned by vector ##\vec{A} ## and ##\vec{B}##, we can take the derivative:

the volume is ##V=\epsilon_{ijk} A^kB^j##
if you take the ordinary derivative of the volume ##\dfrac {dV} {d\lambda} ##

and this implies you will take the ordinary derivative of ##A^i##(as a result of product rule) which is ##\dfrac{dA^k}{d\lambda} ##
however this is just part of the ##\nabla_vA##:

##[∇vA]^k=\dfrac{dA^k}{d\lambda}[1.]+v^j\gamma^{k}_{ij}[2]=v^j\dfrac{dA^k}{dx^j} + v^j\gamma^{k}_{ij}##where##\gamma^{k}_{ij} ##is the connection factor that is missed out and ##v^j \dfrac{d}{dx^j}##is equal to ##\frac{d}{d\lambda}##.It is shown that the ordinary derivative of ##A^i## is just[1.]and[2] is neglected.
[1.] is just the ordinary derivative part of the volume derivation
[2] is the whole derivative which includes connection factor
it is clear that [1.] is not equal to [2]
Therefore##[∇vA]^k##is not equal to ##\dfrac{dA^k}{d\lambda}##
Follow the similar line of reasoning,i think ##\ddot{S^{\mu_j} _j} ##=##\dfrac{d^2(s^{u_j})}{d\lambda^2}## should not be equal to##[\nabla_v\nabla_vS]^{u^j}## ,i am not sure why they are equal##\ddot{S^{u_j} _j}= \dfrac{d^2(s^{u_j})}{d\lambda^2}= ? ? [∇v∇vS]^{uj}= R^{u_j}{}_{xyz} s^y_j v^z y^x##could anyone help me please

 

[PeterDonis]

The former one is just second ordinary derivative

No, it isn't. It is the derivative along a curve: whatever curve you are parallel transporting vectors and angles along using the Levi-Civita connection. The double dot above ##s## means the second derivative with respect to the curve parameter.

 

[bres gres]

No, it isn't. It is the derivative along a curve: whatever curve you are parallel transporting vectors and angles along using the Levi-Civita connection. The double dot above ##s## means the second derivative with respect to the curve parameter.

i see. However the problem is not solved yet.
it seems the presenter is not correct to set ##\ddot{S^{u_j} _j}= [∇v∇vS]^{uj}## as they are different object.(i am not sure??may be he is correct)
the former one is just part of the product: ##\dfrac{dV}{d\lambda} =\epsilon_{ijk} deg(\sqrt(g))[\dfrac{dS^{u_i} _i}{d\lambda}]S^{u_j} _j##

and this $$[\dfrac{dS^{u_i} _i}{d\lambda}]$$ is not equal to$$ [∇vS]^{ui}$$

if this is not the same,then i think the second order derivative one would not be the same as well :(

 

[bres gres]

No, it isn't. It is the derivative along a curve: whatever curve you are parallel transporting vectors and angles along using the Levi-Civita connection. The double dot above ##s## means the second derivative with respect to the curve parameter.

thank for correcting my mistake.
i should said it is not "ordinary" but "normal-type derivative along the curve"(i mean they don't involve the derivative of basis vector ,therefore there is no connection coefficient involved.

 

[PeterDonis]

it seems the presenter is not correct

I don't see anything wrong with the overall logic in the presentation. Some of the notation is confusing to me.

they are different object

He's not setting them equal because they are the same object. He's setting them equal because the fact that the volume is preserved by parallel transport along a geodesic imposes a relationship between them.

"normal-type derivative along the curve"(i mean they don't involve the derivative of basis vector ,therefore there is no connection coefficient involved.

This is not correct. There are connection coefficients involved when you write the derivative along the curve in terms of coordinate derivatives. They are not independent of each other.