- #1
shadi_s10
- 89
- 0
Hi everyone!
again d'inverno!
to tell the truth I don't really understand what is going on in the cauchy problem!
1)
in section 13.5 "the cauchy problem", it is said that the field equations can be written as the forms in 13.12 to 13.14
can anyone tell me how?
actually I tried to use the riemannian tensor : R_abcd
then I tried to contract indices a and c
but there are some gamma terms which I don not know what to do with.
2)
moreover it is said that if you use the equation that transforms g_ab to g_ab prime (at the end of page 175) , you can get to 13.18
I do not understand how is this one possible:
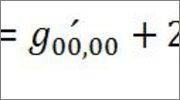
again d'inverno!
to tell the truth I don't really understand what is going on in the cauchy problem!
1)
in section 13.5 "the cauchy problem", it is said that the field equations can be written as the forms in 13.12 to 13.14
can anyone tell me how?
actually I tried to use the riemannian tensor : R_abcd
then I tried to contract indices a and c
but there are some gamma terms which I don not know what to do with.
2)
moreover it is said that if you use the equation that transforms g_ab to g_ab prime (at the end of page 175) , you can get to 13.18
I do not understand how is this one possible: