- #1
kadaj6
- 31
- 0
ok, so I have a list of students with GPA, I checked the probability plot and I think its a Exponential distribution, take a look:
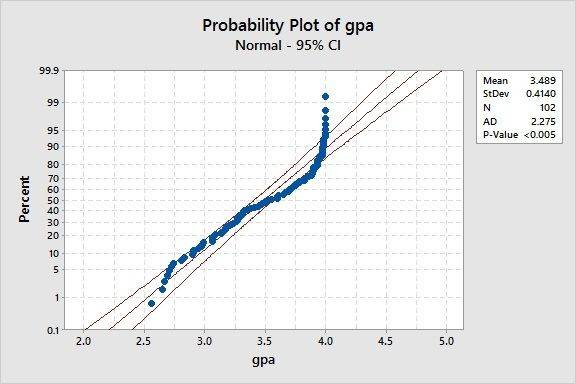
So I am given a χ-bar to prove, and I have to prove or test it with three different types of test, I don't know which ones or how to do them in miniTab software.
please help me.
So I am given a χ-bar to prove, and I have to prove or test it with three different types of test, I don't know which ones or how to do them in miniTab software.
please help me.