Some questions about Fourier series

[baby_1]

Hi,
First of all, I want to say that I know how can define and calculate Fourier coefficients but I have some question about the final presentation of Fourier and half-period or unknown period functions.
1)In this function how can we define T?

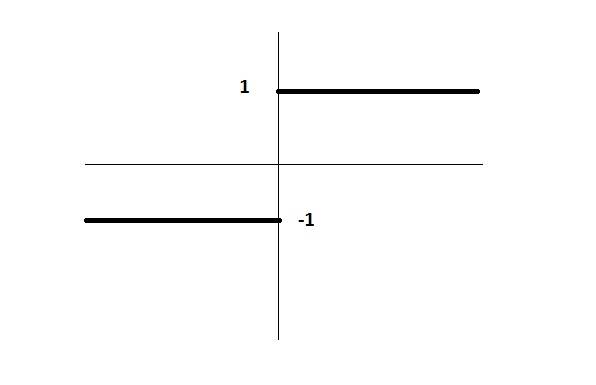
2)for above diagram, in a book, they define f(t) as
f(t)=cos(at)-(1/3)cos(3at)+...
but my question is, Isn't the function f(t) even? but the original shape is odd?
how would it be possible that we present a Sin function into Cos functions?
because for odd function we have a Fourier series like
[tex]f(t)=\sum_{n=1}^{\infty}B_{n}Sin(\omega_{0}((2n+1)t)=B_{0}Sin(\omega_{0}t)+B_{0}Sin(3\omega_{0}t)+...[/tex]

3)why in most references the writer prefer to write even function for half-range expansion instead of odd half-range expansion of a real systems?

Thanks

 

[mfb]

There is a difference between the Fourier transformation of periodic signals (where your formula and questions comes from) and general functions (what is done here).

 

[FactChecker]

For question 2, I believe you are correct. The expansion should use sine.

 

[baby_1]

Thanks for your replay.
Yes, I was wondered why the writer used Fourier series for a non-periodic function and why she/he uses the cos function instead of Sin.
you can see the pdf of the page in attachment.

https://ufile.io/95xlo