Solving for tan γ: Understanding the Relationship between d/l and h/l"

[Expat09]

This is more a question about how the problem is written, rather than a question about how to do the problem

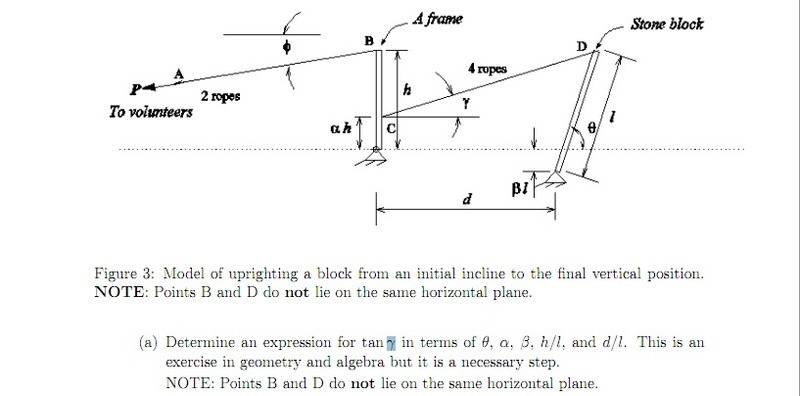
Why do they ask for tan γ in terms of d/l and h/l, rather than d and h? Is there some relation that I'm just not seeing? I'm pretty sure I know how to do the problem in terms of d and h, but the d/l and h/l terms are throwing me off

 

[Ignea_unda]

Welcome to PF, Expat09.

If you look at all the rest of the terms, all of them are dimensionless. By this I mean, they have no units.

[itex] \theta[/itex] is in radians, which are dimensionless
[itex] \alpha[/itex] and [itex] \beta[/itex] are just constants to scale h and l.

Therefore, to make h and d dimensionless, the author chose a common length, l, to make it so there are no units for d/l and h/l.

Does this help at all?