- #1
Rockdog
- 23
- 0
Picture is attached as follows:
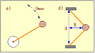
A 480 gm rock is whirled on the end of a string 47 cm long which will break under a tension of 27 N.
a) What is the highest speed the rock can reach before the string breaks? (Neglect gravity.)
b) If two other strings identical to the first were attached to the rock, how fast could the rock be whirled before the three strings would break?
Next the rock is held by two of the same 47 cm strings with ends 56 cm apart and whirled in a circle between them. Neglect gravity.
c) What is the radius of the circle of motion?
d) Now what is the maximum speed the rock can have before the string breaks?
--------------
I'm stuck on part d, but I can go over a-c. Maybe that might help me solve c.
a) Well, the first thing I did was convert grams to kilograms and cm to meters. Then by using this equation, F=(m*v^2)/R
where F=force
m=mass
v=velocity
R=radius, i get V=5.14 m/s
b) Same equation as above, except force now equals 81N (3*27)
answer is 8.91 m/s
c) This I drew a triangle. Since it is isoceles, I figured out that height (radius) = sqrt(47^2-.25*56^2) =>37.7 cm as my radius.
d) Here I'm stuck. I know I can use the centripetal equations: a=v^2/R or F=(m*v^2)/R, but how to go about it I'm unsure about it.
I did draw a triangle, where the hypothenuse was 47, the base is 37.7 cm..and since two angles are 70 and 90 degrees, the last angle is 20 degrees. So I did 47 sin 20 to get the x component, which turned out to be 16.07 cm. Whether this can be of any use to me, I don't know. The hint tells me to break the tensions into their components, but then what?
A 480 gm rock is whirled on the end of a string 47 cm long which will break under a tension of 27 N.
a) What is the highest speed the rock can reach before the string breaks? (Neglect gravity.)
b) If two other strings identical to the first were attached to the rock, how fast could the rock be whirled before the three strings would break?
Next the rock is held by two of the same 47 cm strings with ends 56 cm apart and whirled in a circle between them. Neglect gravity.
c) What is the radius of the circle of motion?
d) Now what is the maximum speed the rock can have before the string breaks?
--------------
I'm stuck on part d, but I can go over a-c. Maybe that might help me solve c.
a) Well, the first thing I did was convert grams to kilograms and cm to meters. Then by using this equation, F=(m*v^2)/R
where F=force
m=mass
v=velocity
R=radius, i get V=5.14 m/s
b) Same equation as above, except force now equals 81N (3*27)
answer is 8.91 m/s
c) This I drew a triangle. Since it is isoceles, I figured out that height (radius) = sqrt(47^2-.25*56^2) =>37.7 cm as my radius.
d) Here I'm stuck. I know I can use the centripetal equations: a=v^2/R or F=(m*v^2)/R, but how to go about it I'm unsure about it.
I did draw a triangle, where the hypothenuse was 47, the base is 37.7 cm..and since two angles are 70 and 90 degrees, the last angle is 20 degrees. So I did 47 sin 20 to get the x component, which turned out to be 16.07 cm. Whether this can be of any use to me, I don't know. The hint tells me to break the tensions into their components, but then what?