Solutions of the schrödinger eq. for a potential step

[71GA]

Lets say we have a potential step as in the picture:

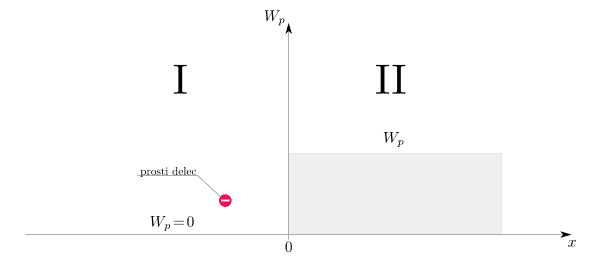
In the region I there is a free particle with a wavefunction ##\psi_I## while in the region II the wave function will be ##\psi_{II}##. Let me now take the Schrödinger equation and try to derive ##\psi_I## which bugs me:

\begin{align}
&~~W \psi = -\frac{\hbar^2}{2m}\, \frac{d^2 \Psi}{d\, x^2} + W_p \psi ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\nonumber \\
&~~W \psi = -\frac{\hbar^2}{2m}\, \frac{d^2 \Psi}{d\, x^2}\nonumber \\
&\frac{d^2 \Psi}{d\, x^2} = -\frac{2m W}{\hbar^2}\,\psi \nonumber\\
{\scriptsize \text{DE: }} &\boxed{\frac{d^2 \Psi}{d\, x^2} = -\mathcal L\,\psi}~\boxed{\mathcal{L} \equiv \sqrt{\tfrac{2mW}{\hbar^2}}} \nonumber\\
&~\phantom{\line(1,0){18.3}}\Downarrow \nonumber\\
{\scriptsize \text{general solution of DE: }} &\boxed{\psi_{I} = C \sin\left(\mathcal{L}\, x \right) + D \cos \left(\mathcal{L}\, x \right)}\nonumber
\end{align}

I got the general solution for the interval I, but this is nothing like the solution they use in all the books: ##\psi_{I} = C e^{i\mathcal L x} + D e^{-i \mathcal L x}## where ##\mathcal L \equiv \sqrt{{\scriptsize 2mW/\hbar^2}}##. I have a personal issue with this because if ##x= -\infty## part ##De^{-i \mathcal L x}## would become infinite and this is impossible for a wavefunction! I know that i would get exponential form if i defined constant ##\mathcal L## a bit differently as i did above:

\begin{align}
{\scriptsize \text{DE: }} &\boxed{\frac{d^2 \Psi}{d\, x^2} = \mathcal L\,\psi}~\boxed{\mathcal{L} \equiv -\sqrt{\tfrac{2mW}{\hbar^2}}} \nonumber\\
&~\phantom{\line(1,0){18.3}}\Downarrow \nonumber\\
{\scriptsize \text{general solution of DE: }} &\boxed{ \psi_{I} = C e^{\mathcal L x } + D^{-\mathcal L x} }\nonumber
\end{align}

This general solution looks more like the one they use in the books but it lacks an imaginary ##i## and ##\mathcal L## is defined with a - while in all the books it is positive. Could anyone tell me what am i missing here so i could connect all this into a solid one piece of knowledge?

 

[bp_psy]

I have a personal issue with this because if ##x= -\infty## part ##De^{-i \mathcal L x}## would become infinite and this is impossible for a wavefunction! I know that i would get exponential form if i defined constant ##\mathcal L## a bit differently as i did above:
\end{align}

The problem is here :
[itex]lim_{x-> \infty} e^{icx} \neq \infty[/itex]
Use the fact that:
e^(icx)=cos(cx)+isin(cx)

 

[71GA]

The problem is here :
$$lim_{x-> \infty} e^{icx} \neq \infty$$
Use the fact that:
$$e^{icx}=\cos(cx)+i\sin(cx)$$

That is eulers formula i know and i can ALMOST derive the connection between the example used in books: ##\scriptsize \psi_I = Ce^{i\mathcal L x} + De^{-i \mathcal L x}## and the first general solution to the DE: ##\scriptsize \psi_I = C\cos (\mathcal L x) + D \sin (\mathcal L x)##.

Here it goes:

$$
\scriptsize
\begin{split}
\underbrace{Ae^{i\mathcal L x} + B e^{-i \mathcal L x}}_{{\scriptsize \text{used in the books}}} = A \cos(\mathcal L x) +A i \sin (\mathcal L x) + B \cos(\mathcal L x) - B i \sin(\mathcal L x) = \underbrace{(A+B)}_{\equiv C} \cos(\mathcal L x) + \underbrace{(A-B)}_{\equiv D} i \sin (\mathcal L x) \neq \underbrace{C\cos (\mathcal L x) + D \sin (\mathcal L x)}_{{\scriptsize \text{solution to the DE}}}
\end{split}
$$

I can notice that the function used in books is NOT equal to the solution to the DE. It is diffrent for an imaginary number ##i##... Here is allso one small snippet from Griffith where he doesn't use ##i##. Take a closer look to the eq. 2.149. I am sorry for posting a snippet, i can remove it if necessary. So my question is why or how does ##i## dissapear?

 

[bp_psy]

You are right except that D=(A-B)i, the i is included there and the two forms of the solution are equivalent.

 

[HomogenousCow]

The constants don't have to be real.

 

[HomogenousCow]

I got the general solution for the interval I, but this is nothing like the solution they use in all the books: ##\psi_{I} = C e^{i\mathcal L x} + D e^{-i \mathcal L x}## where ##\mathcal L \equiv \sqrt{{\scriptsize 2mW/\hbar^2}}##.

Eulers formula.

 

[71GA]

So if i conclude all this (and please correct me if i am in any way wrong). I have a schrödinger equation which for a free particle can be rearanged like this:
$$
\frac{d^2 \Psi}{d\, x^2} = -\frac{2m W}{\hbar^2}\,\psi
$$
This is ofcourse a differential equation whose general solutions depend on how we define the constant ##\mathcal L##.
\begin{align}
\mathcal L \equiv \sqrt{\frac{2mW}{\hbar^2}} \Longrightarrow \underbrace{\psi = C \sin(\mathcal L x) + D \cos (\mathcal L x)}_{\text{1st general solution where $\mathcal L$ is real}}~~~~~~~~\mathcal L \equiv \sqrt{-\frac{2mW}{\hbar^2}} \Longrightarrow \!\!\!\!\!\!\!\!\!\!\!\!\!\!\underbrace{\psi = C e^{\mathcal L x} + D e^{\mathcal L x}}_{\text{2nd general solution where $\mathcal L$ is complex}}
\end{align}
We choose 1st solution which has real ##\mathcal L## and a complex constant ##D## (which can be seen from):
$$
\scriptsize
\begin{split}
\!\!\underbrace{A}_{\text{real}}\!e^{i\mathcal L x} + \!\!\underbrace{B}_{\text{real}}\! e^{-i \mathcal L x}= A \cos(\mathcal L x) +A i \sin (\mathcal L x) + B \cos(\mathcal L x) - B i \sin(\mathcal L x) = \underbrace{(A+B)}_{\equiv C} \cos(\mathcal L x) + \underbrace{(A-B)\,i}_{\equiv D} \sin (\mathcal L x) = C\cos (\mathcal L x) + \!\!\!\!\underbrace{D}_{{\scriptsize \text{complex}}}\!\!\! \sin (\mathcal L x)
\end{split}
$$
From above equation it can be seen that i can write ##\psi = C \sin(\mathcal L x) + D \cos (\mathcal L x)## in a form ##Ae^{i\mathcal L x} + Be^{-i \mathcal L x}## where ##A## and ##B## are real and ##\mathcal L## is also real ##{\scriptsize \mathcal L \equiv \sqrt{2mW/\hbar^2}}##. Please correct me if i am wrong or confirm my assumptions.

 

[bp_psy]

Neither constant are (C,D) necessarily real or complex they are determined by your boundary conditions.
The usual argument in a ODE class is that a second order ODE with a characteristic equation with complex roots we have:
[itex]f(x)=e^{(a+bi)x}[/itex]
[itex]g(x)=e^{(a-bi)x}[/itex]
as solutions. Then by superposition we can get two other solutions

[itex]u(x)=f(x)+g(x)=e^ax(e^{ibx}+e^{-ibx})=2e^{ax} cos(bx)[/itex]
[itex]v(x)=f(x)-g(x)=e^ax(e^{ibx}+e^{-ibx})=2i e^{ax} sin(bx)[/itex]
Since the a solution multiplied by a real or complex constant is still a solution we can ignore the constants,we get the two solutions
[itex]u(x)=e^{ax} cos(bx)[/itex]
[itex]v(x)= e^{ax} sin(bx)[/itex]
Then the general solution by superposition will be :
[itex]v(x)=A e^{ax} cos(bx) +Be^{ax}sin(bx)[/itex] where A and B are two constants set by your boundary conditions.
For physics it is usually better to work with the complex exponential form because the integrals are usually more simple.

 

[71GA]

Thank you. This solved my issue.