- #1
KLscilevothma
- 322
- 0
physics contest -- question 4 (Long question)
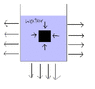
Stationary liquid on Earth exerts pressure on any surface in contact, and the resulting net force is always perpendicular to the suface and pointing away from liquid. For example, as shown by arrows in the figure, the pressure force of water on the sidewalls of the container is horizontal, and the force on the bottom of the container is straight downwards. THe same is applicable to any object in liquid. The pressure force of water on the bottom surface of the cubic objet shown in the figure is straight upwards; the force on the top surface of the cubic object is straight downwards; and the force on the side sufaces of the cubic object is horizontal and pointing towards the cubic object. (The lenghts of the arrows have no rlevance to the strength of the forces).
a) Use the above concept, derive an expression for the pressure at any point in water interms of the depth h of hte point(the distance from the oint to the water surface in contac with air), mass density of water p, and gravity acceleration g on Earth surface. (1 point will be deducted for hint) [I asked for a hint but couldn't get the answer6)]
b) Use the result in (a), prove that the net force of water on the cubic object is equal to pVg and pointing straight upwards, where V is the volume of the cubic object.
c) If the container is placed in a weightless outer space enviroment, what is the pressure of water on the bottom of the container?
d) We now replace the wather and the cubic object with some ideal gas and seal the container. WHen it is in a weightless outer space enviroment, is the pressure of the gas on the container the same as it is on Earth? Explain your answer.
I don't know how to do part a and b.
For a, after chunks of caculations, I got 0.5pgh. I'm sure it is wrong!
c) 0, right?
d) THe same, right ?
Stationary liquid on Earth exerts pressure on any surface in contact, and the resulting net force is always perpendicular to the suface and pointing away from liquid. For example, as shown by arrows in the figure, the pressure force of water on the sidewalls of the container is horizontal, and the force on the bottom of the container is straight downwards. THe same is applicable to any object in liquid. The pressure force of water on the bottom surface of the cubic objet shown in the figure is straight upwards; the force on the top surface of the cubic object is straight downwards; and the force on the side sufaces of the cubic object is horizontal and pointing towards the cubic object. (The lenghts of the arrows have no rlevance to the strength of the forces).
a) Use the above concept, derive an expression for the pressure at any point in water interms of the depth h of hte point(the distance from the oint to the water surface in contac with air), mass density of water p, and gravity acceleration g on Earth surface. (1 point will be deducted for hint) [I asked for a hint but couldn't get the answer6)]
b) Use the result in (a), prove that the net force of water on the cubic object is equal to pVg and pointing straight upwards, where V is the volume of the cubic object.
c) If the container is placed in a weightless outer space enviroment, what is the pressure of water on the bottom of the container?
d) We now replace the wather and the cubic object with some ideal gas and seal the container. WHen it is in a weightless outer space enviroment, is the pressure of the gas on the container the same as it is on Earth? Explain your answer.
I don't know how to do part a and b.
For a, after chunks of caculations, I got 0.5pgh. I'm sure it is wrong!
c) 0, right?
d) THe same, right ?