RC Low Pass Circuit Sine Wave Response

[jaydnul]

TL;DR Summary

RC Low Pass Circuit Sine Wave Response

Hey Everyone,

I am trying to gain a level of fundamental understanding of an RC circuit sine wave response through the mathematics and was wondering if someone could help me work it out.

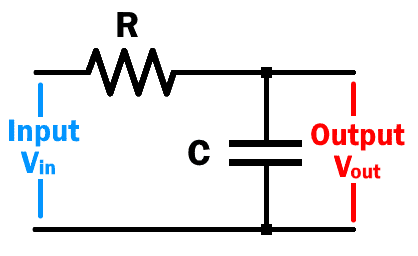
Fundamentally a sine wave is represented by the equation y=-ky'' . When a sine wave is used as the input of an RC low pass filter, you get a sine wave out (just phase and amplitude shifted). So I know that when the input waveform has the form Vin=-kVin'' then somehow the output also retains that relationship, Vout=-kVout''. I am having trouble proving this with the equation that describes an RC circuit response: Vout' = 1/RC*(Vin-Vout).

Any help would be great, thanks!

 

[Baluncore]

Summary:: RC Low Pass Circuit Sine Wave Response

Any help would be great, thanks!

You have a voltage divider. You can use complex numbers; ( R + X·j )
The impedance of R is real; Zr = ( R + 0·j )
The impedance of C is imag; Zc = ( 0 + Xc·j )
Where Xc is the reactance of the capacitor at frequency f.
Xc = –1 / ( 2·π·f·C ); Yes the reactance of C is negative.

The input appears across the sum; Zin = ( R + Xc·j )
The complex input current is; Iin = Vin / ( R + Xc·j )
The output appears across C; Vout = Iin·( 0 + Xc·j )
Vout = Vin·( 0 + Xc·j ) / ( R + Xc·j )
The complex number Vout gives amplitude and phase.

 

[Delta2]

I tried to do it via the response equation and couldn't prove it either. Instead I can prove it via the differential equation that corresponds to this circuit:
From Kirchhoff's voltage law we have: $$V_{in}+R\frac{dq(t)}{dt}+\frac{q(t)}{C}=0$$

Now if ##V_{in}=V_{0in}\sin{\omega t}## then we can prove that the solution to this differential equation is $$q(t)=q_0\sin({\omega t+\phi})$$ where ##q_0## and the phase shift ##\phi## are functions of ##R,C,\omega## iirc it is ##\phi=\arctan{\frac{1}{\omega RC}}##.

Hence the voltage on the capacitor is $$V_{out}=\frac{q(t)}{C}=\frac{q_0}{C}\sin({\omega t+\phi})$$ which is also a sine wave shifted by phase ##\phi##

I can post more details on how we solve that differential equation.

 

[vanhees71]

Just use Kirchhoff's rule integrating along the circuit. You get
$$R i+\frac{Q}{C}=R \dot{Q} + \frac{Q}{C}=V_{\text{in}}=U_0 \exp(\mathrm{i} \omega t),$$
where the physical quantities are always the real parts of the complex auxilliaray quantities introduced above. For the stationary state you can make the ansatz
$$Q(t)=A \exp(\mathrm{i} \omega t),$$
leading to
$$A (\mathrm{i} \omega R+1/C)=U_0 \; \Rightarrow \; A=\frac{U_0 C}{(\mathrm{i} \omega R C+1} = \hat{A} \exp(\mathrm{i} \phi),$$
where [CORRECTED]
$$\hat{A}=\frac{U_0}{\sqrt{\omega^2 R^2+1/C^2}}, \quad \phi = -\arccos \frac{1}{\sqrt{\omega^2 R^2 C^2 +1}}.$$
So we have [corrected]
$$U_C(t)=Q(t)/C=\frac{U_0}{\sqrt{\omega^2 R^2 C^2+1}} \cos(\omega t+\phi).$$
Since ##\phi \in (-\pi,0)## the "voltage" across the capacitor is by a phase shift ##\phi## behind the phase of the external voltage.

 

[jaydnul]

Thanks for all the replies! Just for an intuitive visualization I am more looking for an equation in the form of a differential equation (instead of the solutions to the differential equation), just to show that the relationship between acceleration and voltage remains the same without converting to sines or exp functions. I know that getting a sine wave at the output when there is sine wave at the input must mean the the output voltage retains this voltage/acceleration information.

I understand the phasor/exponential/sinusoidal explanations, but is there a way to prove this without exp or sine functions, just keeping it in the form of the differential equations?

My attempt here:

$$(1) Vin = -k\frac {d^2 Vin} {dt^2}$$
Plugged into the RC circuit equation
$$(2) \frac {d Vout} {dt} = \frac {Vin - Vout}{RC}$$
$$(3) \frac {d Vout} {dt} = \frac {-k\frac {d^2 Vin} {dt^2} - Vout}{RC}$$

Differentiating equation (2)
$$(4) \frac {d^2 Vout} {dt^2} = \frac {\frac {d Vin} {dt} - \frac {d Vout} {dt}} {RC}$$

Then plugging equation (3) into equation (4)

$$(5) \frac {d^2 Vout} {dt^2} = \frac {\frac {d Vin} {dt} - \frac {-k\frac {d^2 Vin} {dt^2} - Vout}{RC}} {RC}$$

Not sure where to go from there, or if I am going in completely the wrong direction...

 

[DaveE]

I think you want to eliminate Vi, like this:

## RCV'_o + V_o = V_i ## and ## RCV'_o + V_o = kV''_i ##

then ## k(RCV'_o + V_o)'' = (RCV'_o + V_o) ##

 

[alan123hk]

where the physical quantities are always the real parts of the complex auxilliaray quantities introduced above. For the stationary state you can make the ansatz

This method is indeed very convenient to find the steady-state solution. But if in complex situations, such as the initial angle of the input sinusoidal voltage is not zero degree, or the initial stored charge of the capacitor is not zero coulomb , then we need to find the complete transient solution of the differential equation under specific initial conditions.

Sorry, if I digress.

Edit : I think the above is not accurate. Regardless of the initial input voltage angle and initial capacitor charge, there will almost certainly be a transient response part. The question is whether we need to find out this part of the equation.

 

[vanhees71]

Thanks for all the replies! Just for an intuitive visualization I am more looking for an equation in the form of a differential equation (instead of the solutions to the differential equation), just to show that the relationship between acceleration and voltage remains the same without converting to sines or exp functions. I know that getting a sine wave at the output when there is sine wave at the input must mean the the output voltage retains this voltage/acceleration information.

I understand the phasor/exponential/sinusoidal explanations, but is there a way to prove this without exp or sine functions, just keeping it in the form of the differential equations?

My attempt here:

$$(1) Vin = -k\frac {d^2 Vin} {dt^2}$$
Plugged into the RC circuit equation
$$(2) \frac {d Vout} {dt} = \frac {Vin - Vout}{RC}$$
$$(3) \frac {d Vout} {dt} = \frac {-k\frac {d^2 Vin} {dt^2} - Vout}{RC}$$

Differentiating equation (2)
$$(4) \frac {d^2 Vout} {dt^2} = \frac {\frac {d Vin} {dt} - \frac {d Vout} {dt}} {RC}$$

Then plugging equation (3) into equation (4)

$$(5) \frac {d^2 Vout} {dt^2} = \frac {\frac {d Vin} {dt} - \frac {-k\frac {d^2 Vin} {dt^2} - Vout}{RC}} {RC}$$

Not sure where to go from there, or if I am going in completely the wrong direction...

Of course, having used the trick with the exponential ansatz for the stationary state, describing the situation after the transients are damped away, you can simply introduce the usual complex impdedances,
$$Z_R=R, \quad Z_C=-\mathrm{i}{\omega C}, \quad Z_L=\mathrm{i} \omega L.$$
Then you can use the usual parallel and series formulae for resistors in DC theory for the impedances in AC theory. The complex amplitudes or effective values (differing just by a factor of ##\sqrt{2}##) for current and "voltage" then fulfill formally Ohm's Law
$$I=U/Z$$
Writing ##Z=|Z| \exp(\mathrm{i} \varphi)## directly provides the magnitude and phase shift of the relation between ##i## and ##U##.

For the example in the OP you have
$$Z=R-\mathrm{i}{\omega C}$$
And thus
$$I=\frac{U}{R-\mathrm{i}/(\omega C)}=\frac{\mathrm{i} \omega C}{1+\mathrm{i} \omega R}.$$
The voltage across the capacitor is
$$U_C=Z_C I=\mathrm{1}{\omega C}=\frac{U}{\mathrm{i} R \omega C+1}.$$
$$U_C=\frac{U}{\sqrt{\omega^2 R^2 C^2+1}} \exp(\mathrm{i} \phi),$$
where
$$\phi=-\arccos\left (\frac{1}{\sqrt{R^2C^2 \omega^2 + 1}} \right).$$
This agrees with my above (now corrected!) calculation.