R^n as a normed space .... D&K Lemma 1.1.7 ....

[Math Amateur]

I am reading "Multidimensional Real Analysis I: Differentiation by J. J. Duistermaat and J. A. C. Kolk ...

I am focused on Chapter 1: Continuity ... ...

I need help with an aspect of Lemma 1,1,7 (iv) ...

Duistermaat and Kolk"s Lemma 1.1.7 reads as follows:

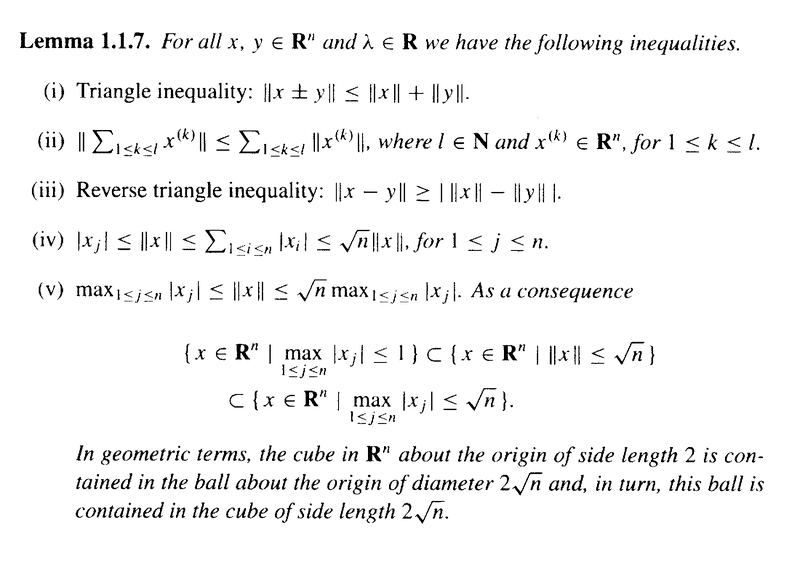
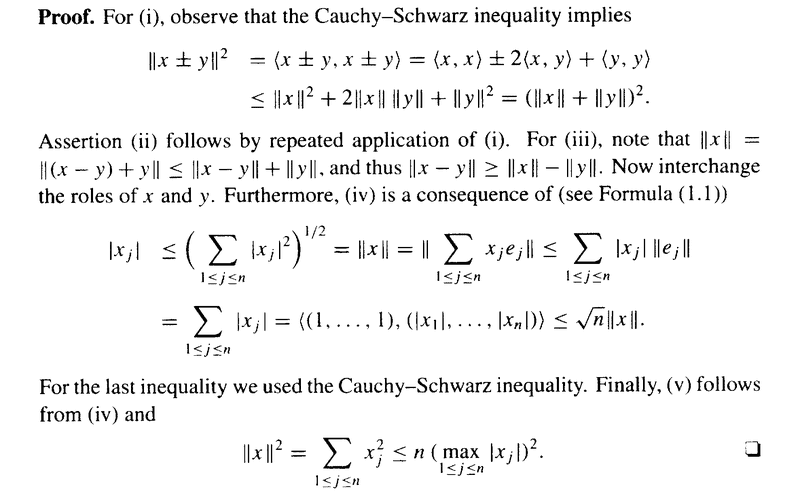
At the start of the proof of (iv) we read the following:

" ... ...##\mid x_j \mid \le \left( \sum_{ 1 \le j \le n } \mid x_j \mid^2 \right)^{ \frac{ 1 }{ 2 } } = \| x \|## ... ... ... "
Suppose now we want to show, formally and rigorously that## \mid x_j \mid \le \left( \sum_{ 1 \le j \le n } \mid x_j \mid^2 \right)^{ \frac{ 1 }{ 2 } }##Maybe we could start with (obviously true ...)

##\mid x_j \mid = ( \mid x_j \mid^2 )^{ \frac{ 1 }{ 2 } } ## ... ... ... ... ... (1)

then we can write

##\mid x_j \mid = ( \mid x_j \mid^2 )^{ \frac{ 1 }{ 2 } } \le ( \mid x_1 \mid^2 + \mid x_2 \mid^2 + \ ... \ ... \ + \mid x_j \mid^2 + \ ... \ ... \ + \mid x_n \mid^2 )^{ \frac{ 1 }{ 2 } }##and we note that##( \mid x_1 \mid^2 + \mid x_2 \mid^2 + \ ... \ ... \ + \mid x_j \mid^2 + \ ... \ ... \ + \mid x_n \mid^2 )^{ \frac{ 1 }{ 2 } } = ( x_1^2 + x_2^2 + \ ... \ ... \ + x_j^2 + \ ... \ ... \ + x_n^2 )^{ \frac{ 1 }{ 2 } } = \| x \| ## ... ... ... ... (3)... BUT ... I worry that (formally anyway) (1) is invalid ... or compromised at least ...

... for suppose for example ##x_j = -3## then ...... we have LHS of (1) = ##\mid x_j \mid = \mid -3 \mid = 3##... BUT ...

RHS of (1) = ##( \mid x_j \mid^2 )^{ \frac{ 1 }{ 2 } } = ( \mid -3 \mid^2 )^{ \frac{ 1 }{ 2 } } = ( 3^2 )^{ \frac{ 1 }{ 2 } } = 9^{ \frac{ 1 }{ 2 } } = \pm 3##My question is as follows:

How do we deal with the above situation ... and

how do we formally and rigorously demonstrate that ##\mid x_j \mid \le \left( \sum_{ 1 \le j \le n } \mid x_j \mid^2 \right)^{ \frac{ 1 }{ 2 } }##Hope someone can help ...

Peter

 

[member 587159]

I can't read your question. The latex does not compile properly.

 

[Math Amateur]

I can't read your question. The latex does not compile properly.

Yes, I know ... just correcting it now ... my apologies ...
Peter***EDIT*** Should be OK now ... apologies for problems ...

 

[member 587159]

I think you misquoted what is written.

It clearly says:

##|x_j| \leq \left(\sum |x_i|^2\right)^{1/2}##

Not:

##|x_j| \leq \sum |x_i|^2##

The former is true, the latter not (Take the vector ##(1/2,0,0, \dots, 0)##, then ##x_1 = 1/2 \geq 1/4)##

 

[Math Amateur]

I think you misquoted what is written.

It clearly says:

##|x_j| \leq \left(\sum |x_i|^2\right)^{1/2}##

Not:

##|x_j| \leq \sum |x_i|^2##

Sorry ... just now corrected that as well ...

Peter

 

[member 587159]

Sorry ... just now corrected that as well ...

Peter

Okay, now I can see what the question is haha.

Step 1: Show that ##\sqrt{\cdot}: \mathbb{R}^+ \to \mathbb{R}## is an order preserving function, i.e. ##a \leq b \implies \sqrt{a} \leq \sqrt{b}##
Step 2: Note that ##|x_j|^2 \leq \sum_i |x_i|^2##
Step 3: Apply step 1: ##|x_j| = \sqrt{|x_j|^2} \leq \sqrt{\sum_i |x_i|^2}##

 

[Math Amateur]

Okay, now I can see what the question is haha.

Step 1: Show that ##\sqrt{\cdot}: \mathbb{R}^+ \to \mathbb{R}## is an order preserving function, i.e. ##a < b \implies \sqrt{a} \leq \sqrt{b}##
Step 2: Note that ##|x_j|^2 \leq \sum_i |x_i|^2##
Step 3: Apply step 1: ##|x_j| = \sqrt{|x_j|^2} \leq \sqrt{\sum_i |x_i|^2}##

Thanks Math_QED ...

Reflecting on what you have said...

Peter

 

[Math Amateur]

Okay, now I can see what the question is haha.

Step 1: Show that ##\sqrt{\cdot}: \mathbb{R}^+ \to \mathbb{R}## is an order preserving function, i.e. ##a < b \implies \sqrt{a} \leq \sqrt{b}##
Step 2: Note that ##|x_j|^2 \leq \sum_i |x_i|^2##
Step 3: Apply step 1: ##|x_j| = \sqrt{|x_j|^2} \leq \sqrt{\sum_i |x_i|^2}##

Hi Math_QED ...

You write:

" ... ... Step 1: Show that ##\sqrt{\cdot}: \mathbb{R}^+ \to \mathbb{R}## is an order preserving function, i.e. ##a < b \implies \sqrt{a} \leq \sqrt{b}## ..."In carrying out Step 1 I am unsure of how to deal with the fact that ##\sqrt{a} = \pm a## and ##\sqrt{b} = \pm b## ... ... can you help?

(Must say that given ##\sqrt{a} = \pm a## ... it doesn't seem as if ##\sqrt{\cdot}## is order preserving ... )

Hope you can help further ...

Peter

 

[member 587159]

Hi Math_QED ...

You write:

" ... ... Step 1: Show that ##\sqrt{\cdot}: \mathbb{R}^+ \to \mathbb{R}## is an order preserving function, i.e. ##a < b \implies \sqrt{a} \leq \sqrt{b}## ..."In carrying out Step 1 I am unsure of how to deal with the fact that ##\sqrt{a} = \pm a## and ##\sqrt{b} = \pm b## ... ... can you help?

(Must say that given ##\sqrt{a} = \pm a## ... it doesn't seem as if ##\sqrt{\cdot}## is order preserving ... )

Hope you can help further ...

Peter

There seems to be a misconception here. ##\sqrt{x} \neq \pm x## (only whenever ##x = 0,1##). It is true that ##\sqrt{x^2} = |x|## though.

Recall that ##\sqrt{x} = y :\iff y^2 = x## by definition.

 

[Math Amateur]

There seems to be a misconception here. ##\sqrt{x} \neq \pm x## (only whenever ##x = 0,1##). It is true that ##\sqrt{x^2} = |x|## though.

Recall that ##\sqrt{x} = y :\iff y^2 = x## by definition.

Hi Math_QED,

You're right of course ... but I think we have to add to your definition that ##y## is non-negative, that is ##y \in ( 0 , \infty )## ... Is that right?

Here is the definition of the square root of a positive real number from Ethan D. Bloch's book: "The Real Numbers and Real Analysis"

Still not sure how to prove that ##\sqrt{\cdot}: \mathbb{R}^+ \to \mathbb{R}## is an order preserving function, i.e. ##a < b \implies \sqrt{a} \leq \sqrt{b}## ...

... BUT ... if the square root of a number is positive ... then surely my equation (1) is valid ...

Peter

 

[member 587159]

Hi Math_QED,

You're right of course ... but I think we have to add to your definition that ##y## is non-negative, that is ##y \in ( 0 , \infty )## ... Is that right?

Here is the definition of the square root of a positive real number from Ethan D. Bloch's book: "The Real Numbers and Real Analysis"View attachment 221204
Still not sure how to prove that ##\sqrt{\cdot}: \mathbb{R}^+ \to \mathbb{R}## is an order preserving function, i.e. ##a < b \implies \sqrt{a} \leq \sqrt{b}## ...

... BUT ... if the square root of a number is positive ... then surely my equation (1) is valid ...

Peter

Yes, that definition is completely correct (at least in the context of real numbers), but contains something that should be proven, namely that the number x is unique.

I'm not sure either why it excludes the possibility that ##p=0##, since clearly ##0^2 = 0##

Well, let's start with the definition you provide.

Suppose ##0 \leq a \leq b##. By definition, there exist positive numbers ##x,y \in \mathbb{R}^+## such that ##a = x^2## and ##b = y^2##. That ##a \leq b## means exactly that ##x^2 \leq y^2## or equivalently ##x^2 - y^2 = (x-y)(x+y) \leq 0##

Can you proceed now? You have to show that ##x \leq y##

Hint 1: You will have to continue from ##(x-y)(x+y) \leq 0##
Hint 2: When is a product of 2 real numbers negative?

EDIT: Also, I made a small typo when writing the order preserving property:

##a < b## needs to be replaced by ##a \leq b##, so we must prove ##a \leq b \implies \sqrt{a} \leq \sqrt{b}##

 

[Math Amateur]

Hi Math_QED ,

Thanks for the hints ...

Well ... we want to show that for ##a \ge 0## and ##b \ge 0## that we have

##a \le b \Longrightarrow \sqrt{a} \le \sqrt{b}## ... ... ... ... ... (1)

Now put ##a = x^2## and ##b = y^2 ## ... ... ... then (1) becomes ... ... ...

##x^2 \le y^2 \Longrightarrow x \le y## ... ... ... ... ... (2)

Now ... ... ##x^2 \le y^2 \Longrightarrow ( x - y ) ( x + y ) \le 0## ... ... ... ... ... (3)

But ... ... ##x + y \ge 0## ... ... ... ... ... (4)

Hence we have ... ... (3), (4) ##\Longrightarrow ( x - y ) \le 0 \ \ \Longrightarrow x \le y## ...Is that correct?

Peter

 

[member 587159]

Hi Math_QED ,

Thanks for the hints ...

Well ... we want to show that for ##a \ge 0## and ##b \ge 0## that we have

##a \le b \Longrightarrow \sqrt{a} \le \sqrt{b}## ... ... ... ... ... (1)

Now put ##a = x^2## and ##b = y^2 ## ... ... ... then (1) becomes ... ... ...

##x^2 \le y^2 \Longrightarrow x \le y## ... ... ... ... ... (2)

Now ... ... ##x^2 \le y^2 \Longrightarrow ( x - y ) ( x + y ) \le 0## ... ... ... ... ... (3)

But ... ... ##x + y \ge 0## ... ... ... ... ... (4)

Hence we have ... ... (3), (4) ##\Longrightarrow ( x - y ) \le 0 \ \ \Longrightarrow x \le y## ...Is that correct?

Peter

Yes, your proof is correct!

Can you proceed with the original problem now?

 

[Math Amateur]

Yes ... OK with that now ...

Thanks ...

Peter