Question on conservation of angular momentum

[Jeremy1986]

Dear guys,
Recently, i am confused with a problem in my textbook of mechanics. The question is,
suppose there is a disk, placed horizontally, rotate about its center with angular velocity ω. A ball move with respect to the center of the disk in a trace of Archimedean spiral r=αθ. The angular momentum of the ball is conserved with respect to the center O. What is the real force F_θ and F_r acting on that ball ?

this is the question and the solution given in the textbook, since they are written in chinese, i translate it into english

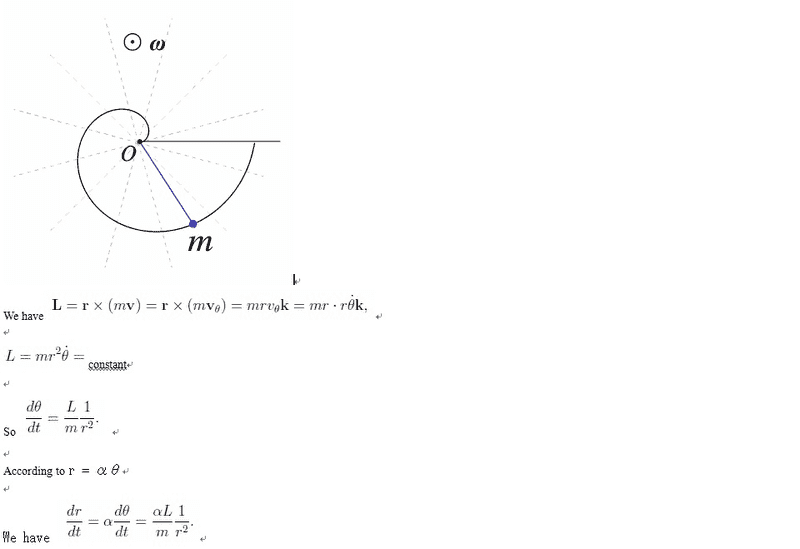
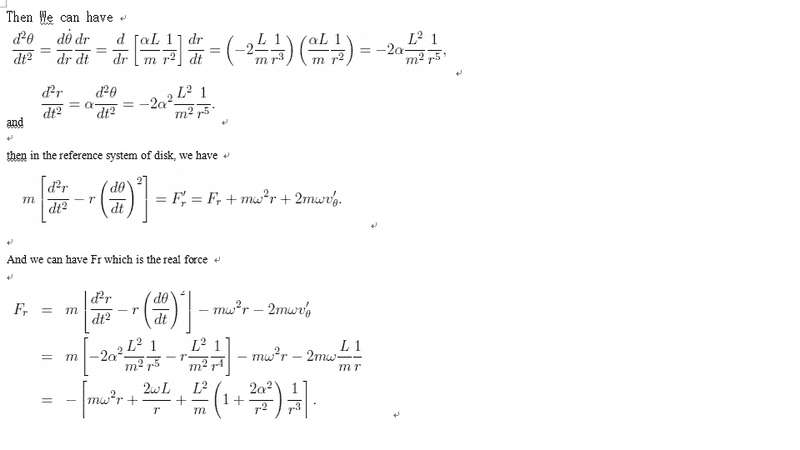
Here is my question. From the solution we can see that the θ is the angular in the disk reference system. And they use the statement that the angular momentum is constant. i don't know which reference system should this statement be applied, whether the disk-reference system which is non-inertial or　the laboratory frame of reference which is inertial?

For me, i think it should be the laboratory frame of reference. and because the disk-reference system is non-inertial, so the angular momentum with respect to the disk-reference system is no longer conserved so it should not be constant anymore

sorry for the long question, i hope i explained both the question and my opinion well. thanks for your help!

 

[Jeremy1986]

i got some idear after posting this thread

the statement "A ball move with respect to the center of the disk in a trace of Archimedean spiral r=αθ,"
here 'with respect to' mean r andθ is in the disk reference of frame.

the conservation of angular momentum can only happens in the disk reference of frame. because in the lab reference frame the net torque can never be zero. but in the disk reference of frame, the net torque can be zero with the help of virtual forces.

 

[PeroK]

i got some idear after posting this thread

the statement "A ball move with respect to the center of the disk in a trace of Archimedean spiral r=αθ,"
here 'with respect to' mean r andθ is in the disk reference of frame.

the conservation of angular momentum can only happens in the disk reference of frame. because in the lab reference frame the net torque can never be zero. but in the disk reference of frame, the net torque can be zero with the help of virtual forces.

You could see this more easily by considering the ball moving out with constant radial velocity ##v_r## relative to the disk. It's position relative to the disk is ##r = v_rt, \ \theta = 0##

In the external frame, it's position is ##r = v_rt, \ \theta = \omega t##, hence ##r = \alpha \theta## with ##\alpha = v_r/ \omega##

Or, turning this round: ##v_r = \alpha \omega##

And, its angular momentum in the external frame is ##L = mrv_{\theta} = mr^2 \omega = m \alpha^2 \omega^3 t^2##

 

[Jeremy1986]

You could see this more easily by considering the ball moving out with constant radial velocity ##v_r## relative to the disk. It's position relative to the disk is ##r = v_rt, \ \theta = 0##

In the external frame, it's position is ##r = v_rt, \ \theta = \omega t##, hence ##r = \alpha \theta## with ##\alpha = v_r/ \omega##

Or, turning this round: ##v_r = \alpha \omega##

And, its angular momentum in the external frame is ##L = mrv_{\theta} = mr^2 \omega = m \alpha^2 \omega^3 t^2##

Thanks PeroK! I was out for the past couple of days, and sorry for the late reply. your reply enlightens me, and i think you are right.
as the statement in the question "The angular momentum of the ball is conserved with respect to the center O", we can get that f^'_θ in the disk-reference frame equals to 0. And this means, as you said,"the ball moving out with constant radial velocity v_r relative to the disk". Thanks again for your kind help!