- #1
Happiness
- 679
- 30
Why isn't (5.298) the following instead?
##K(x, t_1; x', t_0) = \delta(x-x')\,e^{-\frac{i}{\hbar}H(t_1-t_0)}##
My reasoning:
Since [itex]\Psi(x, t_1) = e^{-\frac{i}{\hbar}H(t_1-t_0)}\,\Psi(x, t_0)\\
= e^{-\frac{i}{\hbar}H(t_1-t_0)}\,\int\delta(x-x')\Psi(x', t_0)\,dx'[/itex]
The exponential operator with ##H## is acting on the variable ##x##. So when it is pulled inside the integral, it should just be acting on ##\Psi(x', t_0)## so that after applying ##\delta(x-x')## and integrating, we get the same answer as the one when the exponential operator is acting on ##\Psi(x, t_0)##:
[itex]\Psi(x, t_1) =\int\delta(x-x')e^{-\frac{i}{\hbar}H(t_1-t_0)}\Psi(x', t_0)\,dx'[/itex]
Edit: I believe there is a typo at (5.304). It should be ##(x_n - x_{n-1})## instead of ##(x_n + x_{n-1})##. Correct?



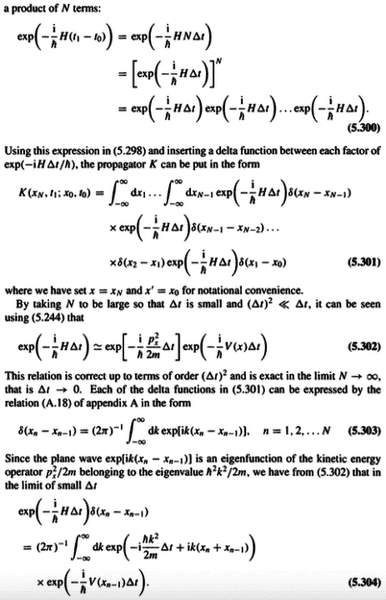
##K(x, t_1; x', t_0) = \delta(x-x')\,e^{-\frac{i}{\hbar}H(t_1-t_0)}##
My reasoning:
Since [itex]\Psi(x, t_1) = e^{-\frac{i}{\hbar}H(t_1-t_0)}\,\Psi(x, t_0)\\
= e^{-\frac{i}{\hbar}H(t_1-t_0)}\,\int\delta(x-x')\Psi(x', t_0)\,dx'[/itex]
The exponential operator with ##H## is acting on the variable ##x##. So when it is pulled inside the integral, it should just be acting on ##\Psi(x', t_0)## so that after applying ##\delta(x-x')## and integrating, we get the same answer as the one when the exponential operator is acting on ##\Psi(x, t_0)##:
[itex]\Psi(x, t_1) =\int\delta(x-x')e^{-\frac{i}{\hbar}H(t_1-t_0)}\Psi(x', t_0)\,dx'[/itex]
Edit: I believe there is a typo at (5.304). It should be ##(x_n - x_{n-1})## instead of ##(x_n + x_{n-1})##. Correct?
Last edited: