Order in Renormalization Theory

[taishizhiqiu]

I am currently studying QFT with 'An Introduction to Quantum Field Theory' by peskin. In part 2 (renormalization) of the book, he introduces counterterms and shows how to compute scattering amplitude with them.
Below are counterterms of [itex]\phi^4[/itex] theory:

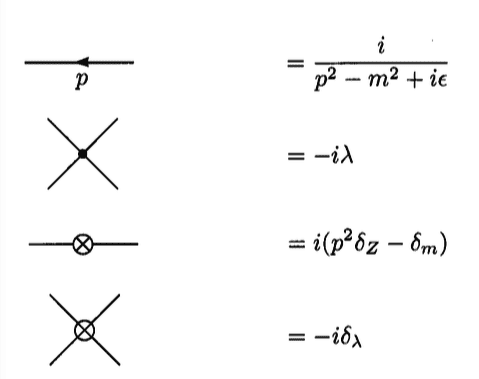
Then he calculates a 2-2 scattering process to the second order:

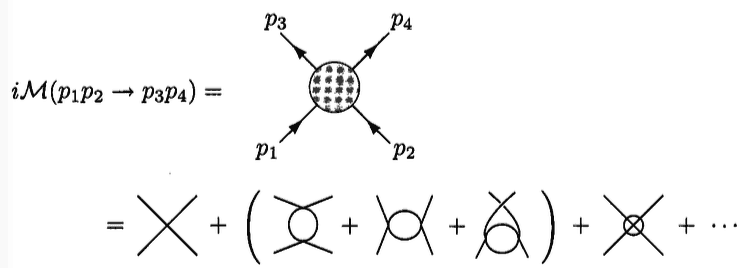
Here I have a few questions:

1. Why the fifth diagram in the second line of the second picture is of the same order to the previous three diagrams?

2. Now that [itex]\delta_m,\delta_Z,\delta_\lambda[/itex] are infinite numbers, how can they use perturbation theory and what is the meaning of order in renormalization perturbation theory?

Edit: should this thread be moved to Homework section? It just cannot be fit into the question structure there.

 

[vanhees71]

It's most simple to look at perturbative renormalization in terms of the finite physical quantities. So you start at tree level. There's no counterterm necessary since you just take the S-matrix elements from your Feynman rules, evaluate cross sections at tree level ("Born approximation") and fit the coupling and masses to some experiment.

Then you go further and do a one-loop calculation. Then you'll find divergent loop integrals, but even if you wouldn't have divergences, you'd have to refit your parameters to the experiment again, i.e., you need counter terms in order to readjust the parameters in terms of their physical quantities. At the order given by the Feynman diagrams, both your (divergent) loop diagrams and the corresponding counter terms are of order ##\hbar## (relative to the tree-level order). Then you go on, and do two-loop diagrams. After taking into account the counter terms of the one-loop result for the subdivergences according to Zimmermann's forest formula you are again left with local overall counterterms which cancel the overall divergences of the two-loop diagrams. They are of the same order ##\mathcal{O}(\hbar^2)## as the (divergent) two-loop diagrams and so on. In this iterative way, using Weinberg's convergence theorem and the BPHZ formalism you can show that ##\phi^4## theory is Dyson renormalizable order by order in perturbation theory, i.e., you only need counter terms of the form already present in the bare Lagrangian, i.e., order by order the renormalization of the wave function norm, mass, and coupling constant is sufficient to get finite results for the S-matrix elements entering observable quantities like cross sections.

 

[taishizhiqiu]

At the order given by the Feynman diagrams, both your (divergent) loop diagrams and the corresponding counter terms are of order ##\hbar## (relative to the tree-level order).

Please explain why the one-loop diagram and counterterm diagram showed in my post is of order [itex]\hbar[/itex](especially the counterterm diagram). Most textbooks set [itex]\hbar=1[/itex] so I have difficulty finding this out.

Will the result of renormalization perturbation theory becomes smaller and smaller order by order? If it is, why? If it is not, what's the meaning of perturbation?

 

[vanhees71]

You can as well take the physical coupling constant ##\lambda## as your counting parameter. In ##\phi^4## theory they are strictly correlated. The ##\hbar## order is given by the number of loops, i.e., each quantum loop in the Feynman diagram enhances its ##\hbar## order by one. Have a look at my QFT manuscript. In one chapter, I reintroduce ##\hbar## to make this counting explicit. The loop expansion is nothing else than the stationary-phase expansion of the path integral to evaluate the effective (quantum) action:

http://fias.uni-frankfurt.de/~hees/publ/lect.pdf

 

[taishizhiqiu]

You can as well take the physical coupling constant ##\lambda## as your counting parameter. In ##\phi^4## theory they are strictly correlated. The ##\hbar## order is given by the number of loops

I don't see any loops in the counterterm diagram(nor any ##\lambda## term), can you show me explicitly?

 

[vanhees71]

Take the example in posting #1. The three one-loop diagrams can be written as ##\mathrm{i} \mathcal{M}=-\mathrm{i} [A(s)+A(t) + A(u)]## with the usual Mandelstam variables ##s##, ##t##, and ##u##.

The one-loop piece ##\Gamma(s)## is logarithmically divergent. In dim. reg you have
##A(s)=-\frac{\lambda^2}{32 \pi \epsilon}+\text{finite}.##
In order to make this finite in the limit ##\epsilon=\frac{4-d}{2} \rightarrow 0##, you have to subtract at least this pole term (minimal subtraction scheme), and this is of order ##\lambda^2##, of course.

At the same time, the counterterm are always local terms as in the original expression. Thus in diagrammatic language it's usually drawn as some blob as in posting #1 (last graph). Technically these are the contractions of divergent diagrams in the forest formula.

If you go to higher order, you have to subtract first all subdivergences (which can be nested but not overlapping, which was the great achievement by BPHZ and is the essence of Zimmermann's forest formula). This is done by drawing all bare diagrams and contractions of divergent subdiagrams. The subdiagrams are of lower order and thus you know the counter terms and thus you know the Feynman rules for the contractions, which now stand for counter terms. These make all the subdivergences finite, and you are left with an overall divergence, which is again a local term as appearing in the original Lagrangian (that's the 2nd essence of the forest formula). In this way you can go inductively from one to the next loop (expansion parameter ##\hbar##) or coupling-constant order (expansion parameter ##\lambda##), which are equivalent for ##\phi^4## theory.

For details of the calculation, see p. 157 of my lecture notes. I just realize that I have to repair the diagram on p. 157. I hope, I can manage this right away!

 

[taishizhiqiu]

Take the example in posting #1. The three one-loop diagrams can be written as ##\mathrm{i} \mathcal{M}=-\mathrm{i} [A(s)+A(t) + A(u)]## with the usual Mandelstam variables ##s##, ##t##, and ##u##.

The one-loop piece ##\Gamma(s)## is logarithmically divergent. In dim. reg you have
##A(s)=-\frac{\lambda^2}{32 \pi \epsilon}+\text{finite}.##
In order to make this finite in the limit ##\epsilon=\frac{4-d}{2} \rightarrow 0##, you have to subtract at least this pole term (minimal subtraction scheme), and this is of order ##\lambda^2##, of course.

At the same time, the counterterm are always local terms as in the original expression. Thus in diagrammatic language it's usually drawn as some blob as in posting #1 (last graph). Technically these are the contractions of divergent diagrams in the forest formula.

If you go to higher order, you have to subtract first all subdivergences (which can be nested but not overlapping, which was the great achievement by BPHZ and is the essence of Zimmermann's forest formula). This is done by drawing all bare diagrams and contractions of divergent subdiagrams. The subdiagrams are of lower order and thus you know the counter terms and thus you know the Feynman rules for the contractions, which now stand for counter terms. These make all the subdivergences finite, and you are left with an overall divergence, which is again a local term as appearing in the original Lagrangian (that's the 2nd essence of the forest formula). In this way you can go inductively from one to the next loop (expansion parameter ##\hbar##) or coupling-constant order (expansion parameter ##\lambda##), which are equivalent for ##\phi^4## theory.

For details of the calculation, see p. 157 of my lecture notes. I just realize that I have to repair the diagram on p. 157. I hope, I can manage this right away!

I have read much more about renormalization now and I know how infinities are cured, but I am still confused.

What justifies the renormalized perturbation theory? Now that infinities are involved, I cannot expect a convergent sequence.