- #1
Rectifier
Gold Member
- 313
- 4
The problem
Consider field ##(F, +, \cdot), \ F = \{ 0,1,2,3 \}##
With the addition table:
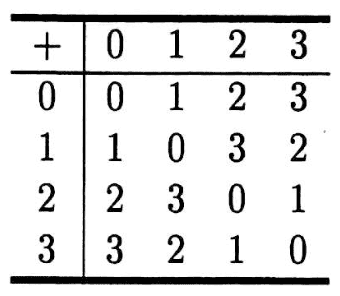
Find a multiplication table.
The attempt
Please read the most of my answer before writing a reply.
My solution was
$$
\begin{array}{|c|c|c|}
\hline \cdot & 0 & 1 & 2 & 3 \\\hline
0 & 0 & 0 & 0 & 0 \\\hline
1 & 0 & 1 & 2 & 3 \\\hline
2 & 0 & 2 & 0 & 2 \\\hline
3 & 0 & 3 & 2 & 1 \\\hline
\end{array}
$$
The solution in the book was
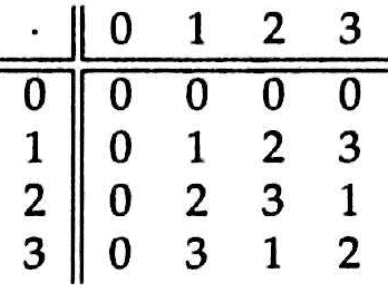
I don't really understand how they get ##2 \cdot 2 = 3## and ##3 \cdot 3 = 2## and ##3 \cdot 2 = 2 \cdot 3 = 1##. I know that multiplication in a field is commutative so a \cdot b = b \cdot a thus ##3 \cdot 2 = 2 \cdot 3 ## but I don't know why it is 1 and not 2.
Lets take one of these as example:
##2 \cdot 2## is 4 right? Then when we calculate the the remainder in respect to 4 ( as it is 4 elements in the field and a field is by definition a commutative ring, right? and we want the answer to be another element in the ring) so it becomes 0. That is ##R_4(4) = 0##. For ##3 \cdot 3 = 9## which produces the remainder ##R_4(9)=1##.
Could someone please help me with what I am doing wrong and how I should solve it instead? Please be specific. Tell me how I should tackle this problem.I am not asking for a solution but for the procedure for these kinds of problems.
Consider field ##(F, +, \cdot), \ F = \{ 0,1,2,3 \}##
With the addition table:
Find a multiplication table.
The attempt
Please read the most of my answer before writing a reply.
My solution was
$$
\begin{array}{|c|c|c|}
\hline \cdot & 0 & 1 & 2 & 3 \\\hline
0 & 0 & 0 & 0 & 0 \\\hline
1 & 0 & 1 & 2 & 3 \\\hline
2 & 0 & 2 & 0 & 2 \\\hline
3 & 0 & 3 & 2 & 1 \\\hline
\end{array}
$$
The solution in the book was
I don't really understand how they get ##2 \cdot 2 = 3## and ##3 \cdot 3 = 2## and ##3 \cdot 2 = 2 \cdot 3 = 1##. I know that multiplication in a field is commutative so a \cdot b = b \cdot a thus ##3 \cdot 2 = 2 \cdot 3 ## but I don't know why it is 1 and not 2.
Lets take one of these as example:
##2 \cdot 2## is 4 right? Then when we calculate the the remainder in respect to 4 ( as it is 4 elements in the field and a field is by definition a commutative ring, right? and we want the answer to be another element in the ring) so it becomes 0. That is ##R_4(4) = 0##. For ##3 \cdot 3 = 9## which produces the remainder ##R_4(9)=1##.
Could someone please help me with what I am doing wrong and how I should solve it instead? Please be specific. Tell me how I should tackle this problem.I am not asking for a solution but for the procedure for these kinds of problems.