- #1
Math Amateur
Gold Member
MHB
- 3,998
- 48
I am reading "Multidimensional Real Analysis I: Differentiation" by J. J. Duistermaat and J. A. C. Kolk ...
I am focused on Chapter 2: Differentiation ... ...
I need help with the proof of Proposition 2.2.9 ... ...
Duistermaat and Kolk's Proposition 2.2.9 read as follows:

In the above text D&K state that Lemma 1.1.7 (iv) implies Proposition 2.2.9 ...
Can someone please indicate how/why ths is the case ...
Peter
===========================================================================================The above post mentions Lemma 1.1.7 ... so I am providing the text of the same ... as follows:
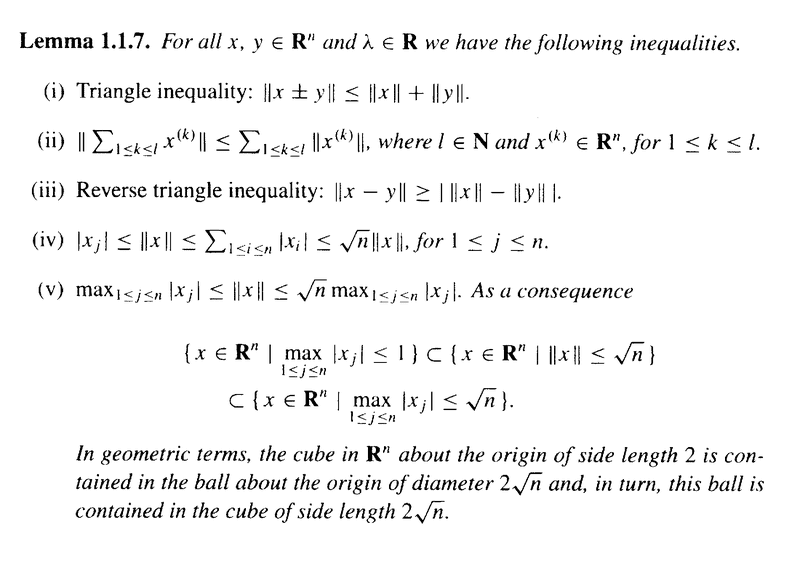
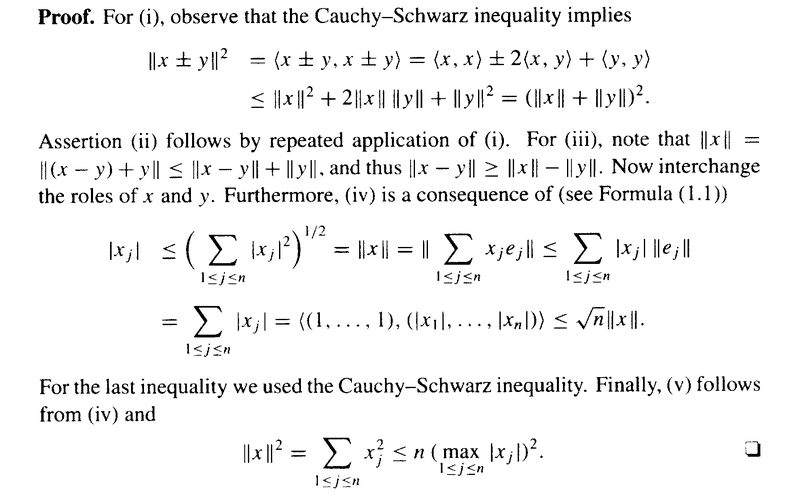
I am focused on Chapter 2: Differentiation ... ...
I need help with the proof of Proposition 2.2.9 ... ...
Duistermaat and Kolk's Proposition 2.2.9 read as follows:
In the above text D&K state that Lemma 1.1.7 (iv) implies Proposition 2.2.9 ...
Can someone please indicate how/why ths is the case ...
Peter
===========================================================================================The above post mentions Lemma 1.1.7 ... so I am providing the text of the same ... as follows:

