MTW Formula 25.38 Coordinate Time

[Passionflower]

In "Gravitation" - Misner, Thorne, Wheeler, the second part of formula 25.38 (first part describes the proper time left till the singularity) seems to suggest it describes some kind of coordinate time left. But the question is what exactly?

Here is the formula:

[tex]
t={\it 2M}\, \left( -2/3\, \left( {\frac {r}{{\it 2M}}} \right) ^{3/2}
-2\,\sqrt {{\frac {r}{{\it 2M}}}}+\ln \left( \left( \sqrt {{\frac {r
}{{\it 2M}}}}+1 \right) \left( \sqrt {{\frac {r}{{\it 2M}}}}-1
\right) ^{-1} \right) \right)
[/tex]

Now this seems to behave well but not close to 2M. For instance if we graph for 2M=1 we get:

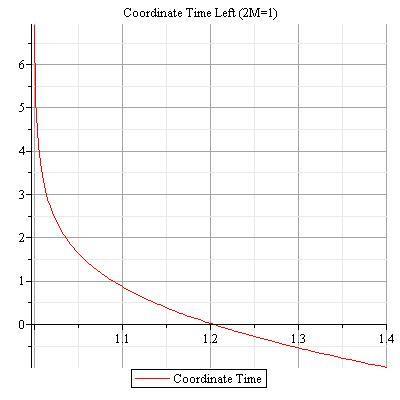
Time left actually becomes zero at around 1.203325645.

Perhaps I am doing something wrong or is there a good explanation?

For comparison proper time left:

 

[PeterDonis]

Take a look at Fig. 25.5 (on the same page as equation 25.38 in my edition of MTW). It should make clearer the meaning of the equations for proper time and coordinate time. The only difference in equation 25.38 is that the zero of proper time is set at the instant when the infalling object reaches r = 0, which would correspond to moving the vertical axis in Fig. 25.5 to the right to the point where the proper time curve intersects r = 0.

 

[Passionflower]

Take a look at Fig. 25.5 (on the same page as equation 25.38 in my edition of MTW). It should make clearer the meaning of the equations for proper time and coordinate time. The only difference in equation 25.38 is that the zero of proper time is set at the instant when the infalling object reaches r = 0, which would correspond to moving the vertical axis in Fig. 25.5 to the right to the point where the proper time curve intersects r = 0.

So you say that 25.38 second part is used in this graph? How?

Are you sure this graph does not handle the cases with an observer free falling starting from a given r as opposed to an observer free falling from infinity which applies to 25.38?

 

[PAllen]

In fig. 25.5, if you move the r/M axis to the right, as suggestet, much of the range of t/M is negative. Thus your graph is plausible. I don't think there is much physical significance to the zero. In some undefined sense it might mean the what 'coordinate time' corresponds to the proper time singularity. However, that can't be physically meaningful, so it is value of convenience for the chosen coordinate time. Prior to adjustment, t ran from zero to infinity. After coordinate change it runs from negative infinity at r infinite, to positive infity at the horizon.

[Edit] I should point out that while I've had MTW since it was first published [blush], I've not read it through, only browsed sections. I looked this section up just now, and Peter Donis explanation seemed very clear.

 

[Passionflower]

In fig. 25.5, if you move the r/M axis to the right, as suggestet, much of the range of t/M is negative. Thus your graph is plausible.

Perhaps we should all first agree what that graph describes. I do not believe this graph applies at all to 25.38. Instead it applies to the case of a free fall from a given r value.

I don't think there is much physical significance to the zero. In some undefined sense it might mean the what 'coordinate time' corresponds to the proper time singularity. However, that can't be physically meaningful, so it is value of convenience for the chosen coordinate time. Prior to adjustment, t ran from zero to infinity. After coordinate change it runs from negative infinity at r infinite, to positive infity at the horizon.

Sorry but I do not understand one bit of what you are saying here.

 

[PeterDonis]

Wonderful that it is crystal clear to you but it is not at all clear to me, which obviously must be my shortcoming. So you say that 25.38 second part is used in this graph? How?

Sorry if I wasn't clear. I didn't mean that equation 25.38 was used in the graph directly; I meant that if you take the vertical axis of the graph (which is time, either proper or coordinate) and move it rightward so it crosses the horizontal axis (which is radial coordinate r) at the point where the proper time curve intersects it, you have a graph which basically illustrates equation 25.38, both parts.

Where does 1.203325645 come from for 2M=1 and t=0? Can you help?

It's just another illustration of the fact that, while it only takes a finite amount of proper time for the falling object to reach r = 0, the falling object never even reaches the horizon at any finite value of coordinate time. In this particular case, the numerical value you obtained could be physically interpreted as follows: put two observers out at r = infinity, and have one fall towards the black hole while the other remains stationary at r = infinity. They both set their clocks to t = minus infinity when the first observer starts to fall. The first observer's clock will read zero just as he hits the singularity at r = 0. When the second observer's clock reads zero, he will "observe" the first observer to be at an r-coordinate of 1.203325645 (assuming 2M = 1). Even as the second observer's clock goes to plus infinity, he will never "observe" the first observer reaching the horizon at r = 1.

(I put "observe" in quotes because to actually define the second observer's "observing" procedure operationally requires care; but basically it means the second observer, after making all measurements and applying all necessary corrections for light travel time, etc., etc., would assign the given r-coordinate to the first observer at the particular t-coordinate corresponding to the given reading on his clock.)

 

[PAllen]

Are you sure this graph does not describe the falling from a given r value as opposed to a free fall from infinity?

Yes, the graph in MTW describes falling from a given r, but it is intuitive (to me) how it would look from infinity.

 

[PeterDonis]

Perhaps we should all first agree what that graph describes. I do not believe this graph applies at all to 25.38. Instead it applies to the case of a free fall from a given r value.

As PAllen said, this is correct, but as MTW note in the text, the physics of the problem is essentially independent of the particular radius at which the object starts falling (they use a capital R for this radius). So they basically take the limit as R -> infinity to obtain equations 25.38; nothing essential is changed, and the graph is still a reasonable representation of what's going on. If you want to be precise, imagine both curves on the graph (with the vertical axis relocated as I described) going out to negative infinity, and increasing vertically without bound as they do; once you get out to large enough negative values, the two graphs basically coincide, so nothing interesting is going on.

 

[Passionflower]

In this particular case, the numerical value you obtained could be physically interpreted as follows: put two observers out at r = infinity, and have one fall towards the black hole while the other remains stationary at r = infinity. They both set their clocks to t = minus infinity when the first observer starts to fall. The first observer's clock will read zero just as he hits the singularity at r = 0. When the second observer's clock reads zero, he will "observe" the first observer to be at an r-coordinate of 1.203325645 (assuming 2M = 1). Even as the second observer's clock goes to plus infinity, he will never "observe" the first observer reaching the horizon at r = 1.

(I put "observe" in quotes because to actually define the second observer's "observing" procedure operationally requires care; but basically it means the second observer, after making all measurements and applying all necessary corrections for light travel time, etc., etc., would assign the given r-coordinate to the first observer at the particular t-coordinate corresponding to the given reading on his clock.)

Thanks, I appreciate the answer!

You response is not directly clear to me, which is obviously my shortcoming, it seems I have to 'sit' on this a little to fully understand it, give me some time to get it.

For any M the result is r(_t=0) = 0.6016628228 M

 

[PAllen]

Sorry but I do not understand one bit of what you are saying here.

Not sure I can help much. The authors are doing two changes:

1) collapse from given r to collapse from infinity;

2) change the zero for proper time to the singularity; all meaningful proper time is then negative.

They then derive the consequences for coordinate time. Their figure 25.5 can be used to suggest what the result will look like. It appears to me that your graph, properly oriented, is what I would expect.

 

[Passionflower]

Here is a graph showing both parts of 25.38 for rs=1

By the way the crossing point is: r=1.439228840

Which is obviously another question, what does it represent?

So we got r=1.203325645 for t=0 and r=1.439228840 for t=tau

When the proper time left is 3/2 the free falling observer reaches the EH and correspondingly the coordinate time is positive infinity.
So does it not seem that when the coordinate time is 0 the free falling observer has not yet reached the EH? On the graph when the coordinate time is zero the proper time left corresponds with -0.8800016760.

It seems I still do not understand what Peter says.

 

[PAllen]

Here is a graph showing both parts of 25.38 for rs=1

View attachment 29173

By the way the crossing point is: r=1.439228840

Which is obviously another question, what does it represent?

So we got r=1.203325645 for t=0 and r=1.439228840 for t=tau

When the proper time left is 3/2 the free falling observer reaches the EH and correspondingly the coordinate time is positive infinity.
So does it not seem that when the coordinate time is 0 the free falling observer has not yet reached the EH? On the graph when the coordinate time is zero the proper time left corresponds with -0.8800016760.

It seems I still do not understand what Peter says.

From your picture (apparently for M=1), proper time of -2/3 corresponds to arrival at the event horizon, proper time zero is the singularity; all this is the aim of the 25.38. The coordinate time at the horizon is positive infinity, as expected, since an outside observer (for whom the given coordinates represent) never sees matter cross the event horizon.

As for relating coordinate time zero for an outside observer to proper time for an infalling observer, personally, I don't view this as having any real physical meaning. Perhaps one can come up with something, but to me the key points are proper time for crossing the event horizon and the singularity, and the asymptotic behavior of coordinate time for an outside observer. All else can be changed at will by arbitrary conventions.

 

[Passionflower]

As for relating coordinate time zero for an outside observer to proper time for an infalling observer, personally, I don't view this as having any real physical meaning. Perhaps one can come up with something, but to me the key points are proper time for crossing the event horizon and the singularity, and the asymptotic behavior of coordinate time for an outside observer. All else can be changed at will by arbitrary conventions.

This is science right?

Are you suggesting, I hope not, that the relationship between the two is hand waving and I should not bother asking such questions?

Clearly there must be a relationship between proper and coordinate time are you disputing that?

For instance for a stationary observer with rs=1 the relationship between coordinate and proper time is:

[tex]{t}^{2}={\tau}^{2} \left( 1-{r}^{-1} \right) ^{-1}[/tex]

 

[PAllen]

This is science right?

Are you suggesting, I hope not, that the relationship between the two is hand waving and I should not bother asking such questions?

Clearly there must be a relationship between proper and coordinate time are you disputing that?

Coordinates are conventions. Invariants are physics. Even more, relating causally disconnected events like an observer approaching and falling through an event horizon to a coordinate convention for an outside observer is truly arbitrary. This whole page in MTW is about a series of arbitrary coordinate transformations that lead to nice math, but have no physical difference from other coordinates. Suppose we are really talking about a collapses from infinity. Do you think it changes physics whether I have coordinate time zero at r=6M versus coordinate time negative infinity at r=infinity?

 

[Passionflower]

Coordinates are conventions. Invariants are physics. Even more, relating causally disconnected events like an observer approaching and falling through an event horizon to a coordinate convention for an outside observer is truly arbitrary. This whole page in MTW is about a series of arbitrary coordinate transformations that lead to nice math, but have no physical difference from other coordinates.

So are you saying that the formula to obtain the coordinate time for a free falling observer from infinity (E=1) for a given r value is numerically useless? It is just "nice math"?

Let me repeat the last question as you did not answer it:

Clearly there must be a relationship between proper and coordinate time are you disputing that?

For instance for a stationary observer with rs=1 the relationship between coordinate and proper time is:

[tex]{t}^{2}={\tau}^{2} \left( 1-{r}^{-1} \right) ^{-1}[/tex]

Is that also "nice math".

 

[yuiop]

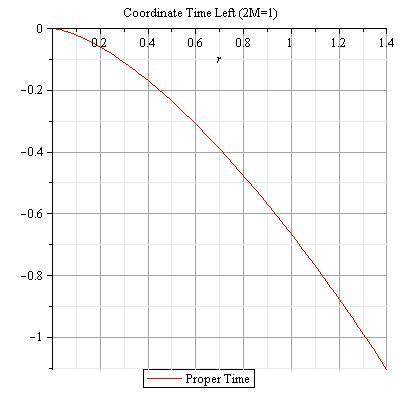
Here is the formula:

[tex]
t={\it 2M}\, \left( -2/3\, \left( {\frac {r}{{\it 2M}}} \right) ^{3/2}
-2\,\sqrt {{\frac {r}{{\it 2M}}}}+\ln \left( \left( \sqrt {{\frac {r
}{{\it 2M}}}}+1 \right) \left( \sqrt {{\frac {r}{{\it 2M}}}}-1
\right) ^{-1} \right) \right)
[/tex]

Now this seems to behave well but not close to 2M. For instance if we graph for 2M=1 we get:

Time left actually becomes zero at around 1.203325645.

Perhaps I am doing something wrong or is there a good explanation?

For comparison proper time left:

This equation is very similar to the one I posted in the Fermi normal thread here https://www.physicsforums.com/showpost.php?p=2923279&postcount=2

[EDIT]Actually it is exactly the same.[/EDIT]

Using this equation for a particle falling from infinity and units of c = 2GM/c^2 = 1:

[tex]
\frac{dt}{dr} = \frac{\sqrt{r}}{ \left( 1 - 1/r \right) }}
[/tex]

and integrating:

[tex]t = \int_{r1}^{r2} \frac{\sqrt{r}}{ \left( 1 - 1/r \right) }} dr = \ln\left(\frac{\sqrt{r2}+1}{\sqrt{r2}-1} \right) - \frac{2}{3}\sqrt{r2}(r2+3) -\left( \ln\left(\frac{\sqrt{r1}+1}{\sqrt{r1}-1} \right) - \frac{2}{3}\sqrt{r1}(r1+3)\right) +C [/tex]

gives the elapsed coordinate time for a particle falling from height r2 to r1. If r1 is set to zero the result is:

[tex]t = \int_{0}^{r2} \frac{\sqrt{r}}{ \left( 1 - 1/r \right) }} dr = \ln\left(\frac{\sqrt{r2}+1}{\sqrt{r2}-1} \right) - \frac{2}{3}\sqrt{r2}(r2+3) -(i\pi) + C [/tex]

Since we are free to add an arbitrary constant of integration (C), we can choose the constant to be [itex]C = +i\pi[/itex] to remove the awkward imaginary factor. When we do this we end up with r=1.203325645 when t=0. Since the constant of integration is arbitrary, there is no special physical significance to the value of r when t=0. Since it takes an infinite amount of coordinate time to reach the event horizon (as you can see by setting r1=1 in the above equation) we cannot conveniently plot the curve to cross the t=0 axis at r=1.

 

[yuiop]

So are you saying that the formula to obtain the coordinate time for a free falling observer from infinity (E=1) for a given r value is numerically useless? It is just "nice math"?

Let me repeat the last question as you did not answer it:

Clearly there must be a relationship between proper and coordinate time are you disputing that?

For instance for a stationary observer with rs=1 the relationship between coordinate and proper time is:

[tex]{t}^{2}={\tau}^{2} \left( 1-{r}^{-1} \right) ^{-1}[/tex]

Is that also "nice math".

For a particle released from infinity, the relationship between the proper time of the falling particle and coordinate time is:

[tex]\frac{dt}{dtau} = \frac{1}{(1-1/r)}[/tex]

and for a particle released from some arbitrary height R the relationship is:

[tex]\frac{dt}{dtau} = \frac{\sqrt{1-1/R}}{(1-1/r)}[/tex]

If you can integrate the above equations you will have your answer.

Note that very close to the event horizon so that [itex]r \approx 1[/itex]:

[tex]\frac{dt}{dtau} \approx \frac{\sqrt{1-1/R}}{0} \approx \infty[/tex]

for any release height R>1.

 

[PeterDonis]

When the proper time left is 3/2 the free falling observer reaches the EH and correspondingly the coordinate time is positive infinity.
So does it not seem that when the coordinate time is 0 the free falling observer has not yet reached the EH?

Yes, this is correct. But instead of "proper time left is 3/2", I would say "proper time = - 3/2" . In other words, the event where the infalling observer crosses the horizon has proper time = - 3/2 but coordinate time positive infinity. So at the given value of r you've calculated, where the coordinate time is 0, the proper time for the infalling observer is something *less* (more negative) than - 3/2. And yes, at this point (meaning, at the event with these coordinates) the infalling observer has not yet crossed the horizon. We could quickly summarize what I've just said as follows, using r for the radius, t for coordinate time, and T for proper time (and assuming 2M = 1):

Event A: "Coordinate time zero", has coordinates r = 1.203325645, t = 0, T < - 3/2 (I can't remember if the exact value has been calculated in this thread).

Event B: "Infalling observer crosses the horizon", has coordinates r = 1, t = + infinity, T = - 3/2.

Event C: "Infalling observer hits the singularity", has coordinates r = 0, t undefined, T = 0.

Note that t, coordinate time, is undefined for event C, because there is a coordinate singularity with Schwarzschild coordinates at r = 2M; the metric coefficient [itex]g_{rr} = \left( 1 - 2M / r \right)^{-1}[/itex] has a "divide by zero error". Technically, this means the coordinate time of Event B is undefined as well, but it seems to be common to state it as + infinity to get across the idea that the observer far away never sees the infalling observer reach the horizon.

All this is just a manifestation of the curvature of the spacetime; coordinate time corresponds to the time experienced by an observer who remains far away from the black hole, whereas the proper time here is the time experienced by the infalling observer. As the latter gets closer to the horizon, the divergence between his experienced time and the time experienced by the observer far away increases, ultimately to infinity when the infalling observer crosses the horizon.

 

[PAllen]

So are you saying that the formula to obtain the coordinate time for a free falling observer from infinity (E=1) for a given r value is numerically useless? It is just "nice math"?

Let me repeat the last question as you did not answer it:

Clearly there must be a relationship between proper and coordinate time are you disputing that?

For instance for a stationary observer with rs=1 the relationship between coordinate and proper time is:

[tex]{t}^{2}={\tau}^{2} \left( 1-{r}^{-1} \right) ^{-1}[/tex]

Is that also "nice math".

The coordinate time assigned by a distant observer is an *interpretation* of information received long after the fact. There are numerous equally valid interpretations (for example, distance defined by radar ranging, luminosity, and parallax will all differ in many GR situations; each is useful for some purposes; differences in distance interpretation leads to differences in time interpretation). I stand by my point of view that any coordinate time assigned to distant events is largely arbitrary, and motivated by convenience for some purpose.

A trivial example: for coordinates on a sphere, is the geometry influenced by what point we choose as a pole? or whether we choose conformal coordinate patches instead of lattitude/longitude? (Conformal coordinates on a sphere, when represented as rectilinear coordinates on a plane, preserve angles; latitude longitude do not; the tradeoff is you need more coordinate patches to cover the sphere).

 

[yuiop]

Event A: "Coordinate time zero", has coordinates r = 1.203325645, t = 0, T < - 3/2 (I can't remember if the exact value has been calculated in this thread).

It is difficult to obtain an exact symbolic solution for the coordinate value of r when t=0 but an iterative solver does confirm that r = 1.203325645*rS = 2.40665129 M is close enough.

The value of T = -3/2 for the proper time to fall from the event horizon to the singularity is not correct however. The correct value is obtained like this:

The velocity of a particle free-falling from infinity in terms of proper time T is:

[tex]\frac{dr}{dT} = -c\sqrt{\frac{r_s}{r}}[/tex]

Rearranging and integrating with respect to r gives:

[tex]\Delta T = \int_{r_1}^{r_2} -\sqrt{\frac{r}{r_s c^2}} = \frac{2r_s}{3c}\left(\left(\frac{r_1}{r_s}\right)^{3/2} - \left(\frac{r_2}{r_s}\right)^{3/2} \right) [/tex]

When [tex]r_2 = r_s[/tex] and [tex]r_1 = 0 [/tex] the result is:

[tex]\Delta T = -\frac{2r_s}{3c} [/tex]

or T = -2/3 when [tex]r_s = c =1[/tex] and not the value -3/2 that has been quoted several times in this thread.

 

[pervect]

Yes, 25.38 gives you the Schwarzschild time coordinate t for an object falling from infinity. The two equations in 25.38 give you the coordinate time t and the coordinate r as a function of tau. The 't' is the time coordinate in the Schwarzschild metric, the 'r' is the radial coordinate in the Schwarzschild metric, and tau is the proper time of the infalling observer. The equations, taken together, implicitly give you a curve paramaterized in tau for an infalling body - i.e. r(tau), and t(tau), which gives you the Schwarzschild coordinates r and t as a function of tau.

And - yes- coordinates do have little physical significance. People can, and do, use all sorts of coordinates to describe black holes. Off the top of my head there are Schwarzschild coordinates, isotropic coordinates, Painleve coordinates, Novikov coordinates, Kruskal-Szerkes coordinates, and Edington-Finklestein coordinates. So the specific coordinate numbers you assign to an event is a matter of convention. Every coordinate system is a "map" of space-time, but the specific numbers you use to label the map are conventional, not physical.

In particular, coordinates, such as the Schwarzschild R coordinate, do _not_ in general represent any sort of physical distance. I'm not sure if you were reading any of the discussion about what distance was in GR or not. A really quick rehash: in relativity, space and time are mixed together, therefore to define distances, one needs to define simultaneity. I'm sure I've made this point before, and I don't want to beat it to death - I don't think you've ever responded to the point.

 

[Passionflower]

We could quickly summarize what I've just said as follows, using r for the radius, t for coordinate time, and T for proper time (and assuming 2M = 1):

Event A: "Coordinate time zero", has coordinates r = 1.203325645, t = 0, T < - 3/2 (I can't remember if the exact value has been calculated in this thread).

Event B: "Infalling observer crosses the horizon", has coordinates r = 1, t = + infinity, T = - 3/2.

Event C: "Infalling observer hits the singularity", has coordinates r = 0, t undefined, T = 0.

Note that t, coordinate time, is undefined for event C, because there is a coordinate singularity with Schwarzschild coordinates at r = 2M; the metric coefficient [itex]g_{rr} = \left( 1 - 2M / r \right)^{-1}[/itex] has a "divide by zero error". Technically, this means the coordinate time of Event B is undefined as well, but it seems to be common to state it as + infinity to get across the idea that the observer far away never sees the infalling observer reach the horizon.

Right as yuiop correctly indicated the proper time at r=1 for rs=1 is -2/3 (not -3/2).

For Event A we get:

Event A: "Coordinate time zero", has coordinates r = 1.203325645, t = 0, T = -0.8800016760

Ok, I finally am getting it as only the difference between two coordinate values have relevance not the absolute value.

I found a related covering of this topic at: http://www.mathpages.com/home/kmath375/kmath375.htm


Thanks everybody for taking the time, it is clear to me now.