Motional EMF in the presence of a time-varying magnetic field

[ocmaxwell]

My question arises from the following problem:

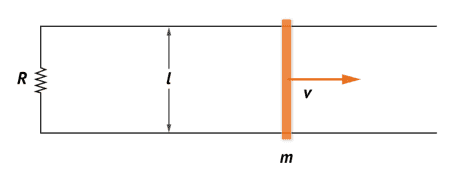
We have a uniform magnetic field into the page, decreasing at a constant rate dB/dt< 0, causing the bar to move to the right. Find the velocity of the bar as a function of the time, and in terms of the known parameters: the resistor R and the separation distance l, and the mass m. See figure below.

My solution:
This is apparently a trivial question, however I have noticed that it's not that trivial as I thought.

What will happen in this situation is that, since the magnetic filed B changes with time and therefore the flux of B through the circuit, there will be and induced current in the circuit, such direction will oppose to the decrease of magnetic flux. It is known that the flux is decreasing so the induced current will be clockwise. This does not stop here: the induced current in presence of the magnetic field will give rise to a magnetic force in the conductors, but there is only one that will move: (the sliding rod). The magnetic force on the sliding bar is to the right (Apply the right hand rule). Notice that as the rod moves the area of the the circuit increases, which is in concordance with the Lenz's Law, but that would also affect the current, the flux, and hence the velocity.

My approach to determine the velocity as a function of the time is by applying the general rule of flux:

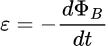
In this case both the area and the magnetic field change with the time, so we have to apply derivative of the product rule:

Being dA/dt = (dA/dx)(dx/dt) if we define the Area as A = lxo + lx, then dA/dx = l and dx/dt = v (which is the velocity of the rod), then the emf will be:
where xo is the initial position of the rod

This will lead to an induced current i = emf/R, a magnetic Force Fm= ilB on the rod, so we can write a differential equation for the motion of the rod in virtue of Newton's second law:

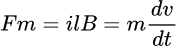
We assumed the increasing direction of the x-axis to the right. Then substituting the induced current into the previous equation we have:

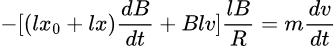
Rearranging the terms we get the differential equation:

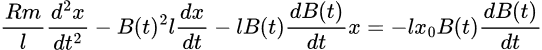
Subjected to the initial conditions: x (t=0) = xo , v(t=0)=0

I am posting this solution, to be considered, first, to see if there is either a concept or a math mistake. I would like to know if my analysis is correct.

I am also interested in getting the solution of the differential equation, if anyone has solved this before.

Any help will be greatly appreciated

Thank you in advance.

 

[kuruman]

It looks OK so far. Since you know that the field decreases at a constant rate, you can write an explicit expression for it, e.g. ##~B(t)=B_0-\beta~t~##, substitute and see what you get. It doesn't seem, though, that the ensuing differential equation is separable.

 

[TSny]

When B reduces to zero, does it remain at zero?

if we define the Area as A = lxo + lx, then dA/dx = l and dx/dt = v (which is the velocity of the rod), then the emf will be:
where xo is the initial position of the rod

View attachment 321738

If you write the area as ##A = lx_0 + lx##, then ##x## is the displacement from ##x_0##. So, your initial condition would be ##x( 0) = 0## instead of ##x(0) = x_0##. Otherwise, I agree with @kuruman, that you're on the right track.

For me, it seems simpler to let ##x## be the position relative to the resistor. So, ##A = lx##. Then ##x(0) = x_0##. With this definition of ##x##, your differential equation will be homogeneous (zero for the right-hand side).

The non-constant coefficients in the differential equation are intimidating. I let Mathematica have a try. If I didn't make any errors, Mathematica gives a fairly compact solution for ##v(t)## in terms of the incomplete Gamma function. [EDIT: Found a sign error in my setup of the differential equation. Mathematica can no longer find a manageable analytic solution to the corrected equation. Looks like we will have to settle for numerical solutions.]

With this solution, you can let Mathematica plot solutions for ##v(t)## up until the time when B = 0.

 

[ocmaxwell]

Thank you both TSny and kuruman for your comments. Yeah, I tried putting the equation in Mathematica, but I am not that good at it; it's giving some errors. I would need to go to a Mathematica forum to ask for help on how to properly set the code to solve the equation.

I would expect a solution in which the velocity behaves like shown in the figure below, in which the velocity is zero al the beginning and approaches to zero when the field vanishes.
In any case thank you both for taking the time to answer the post.

 

[TSny]

Thank you both TSny and kuruman for your comments. Yeah, I tried putting the equation in Mathematica, but I am not that good at it; it's giving some errors. I would need to go to a Mathematica forum to ask for help on how to properly set the code to solve the equation.

With some manipulations, you can see if the differential equation can be written as $$\ddot x - b(t_0 - t)^2\dot x -b(t_0-t)x = 0$$ I could have slipped up, especially with signs. [EDIT: I did make a sign error. The minus sign in front of the second term on the left side should be a plus sign .]The differential equation holds for ##0<t < t_0##, where ##t_0## is the time at which ##B## becomes zero. ##x## is position of the rod relative to ##R##. The constant ##b## is $$b =\frac{\beta^2 l^2}{mR}$$ Here, ##\beta## is @kuruman's symbol for the rate of decrease of ##B##, so that ##B = B_0-\beta t##.

I would expect a solution in which the velocity behaves like shown in the figure below, in which the velocity is zero al the beginning and approaches to zero when the field vanishes.

View attachment 321756

The only way that ##v(t)## could decrease is for the force on the rod to act toward the left. During the time interval that ##B## decreases to zero, is the force ever toward the left?

 

[ocmaxwell]

You are very right though, if the flux is decreasing at a constant rate the force will be pointing toward the right all the time. If the force vanishes as the field does, the velocity wont go to zero, but will approach to a terminal(contant) value.
Thank you for pointing that out. I will continue working out the differential equation and try to solve it to know the actual response. I'll definitely keep you posted on this. Thank you!!

 

[kuruman]

I would need to go to a Mathematica forum to ask for help on how to properly set the code to solve the equation.

Did you mean go here?

 

[ocmaxwell]

lol, yes right there!, Thank you so much kuruman! I did not know there was a forum here for mathematica.

 

[ocmaxwell]

Hello there

I modified the equation as Tsny suggested, and was trying to use mathematica to solve it. I am getting weird results, unless that I am doing something wrong in mathematica. I know this is not a mathematica forum, but please take a look to my code below, any suggestions would be much appreciated. I will include a picture since some characters were modified in the post.

For some reason I am getting zero velocity for all the time.
I gave some real values to the constants to be able to solve the equation. Not sure if the issue has to do with it.

CODE
(*Motion emf when due to a time-varying magnetic field*)
(*Defining Constants*)
Bo= 2;
B[t_]=Bo-(1)*t;
\[Beta] = B'[t];
R= 2;
l=0.1;
xo= 0.25;
Ao= l*xo;
m= 0.25;

(*Constants in the differential equation*)
a=((\[Beta]*l)^2)/(m*R)
b= Bo/\[Beta]

Sol =NDSolve[{x''[t]- a*((b-t)^2)*x'[t]-a*(b-t)*x[t]==-a*xo(b-t),x[0]==xo,x'[0]==0},x,{t,0,10}]

p1=Plot[x'[t]/. Sol, {x, 0,10},
PlotStyle -> {Thick},
PlotRange -> Full,
AxesLabel->{t,"v(t) [m/s]"}]

Thank you in advance

 

[kuruman]

The differential equation holds for ##0<t<t_0##, where ##t_0## is the time at which ##B## becomes zero.

Why? What will happen if the magnetic field goes through zero and starts increasing linearly with the same slope out of the page?

 

[TSny]

I've marked some places that I believe need correction. Earlier, we defined ##\beta## as the constant in ##B(t) = B_0 - \beta t##. Thus, ##\beta = -B'(t)##. So, there is a sign error in your equation for ##\beta##.

As pointed out in post #3, your expression for the area ##A = lx_0 + lx## implies that you are taking ##x## to be the displacement of the rod from its initial position. So, your initial condition should be x[0] = 0. Your symbol ##x_0## is the initial distance of the rod from the resistor, but this is not the initial value of your symbol ##x##.

There appear to be two sign errors in the differential equation:

(1)The right-hand side of your differential equation has the wrong overall sign. I think this is connected to the minus sign in ##\frac{dB(t)}{dt} = - \beta##.

(2) For the sign error on the left-hand side of your differential equation, let's go back to your post #1 where you had

which looks correct. You then rearranged this to

I believe the minus signs on the left side of this equation should actually be plus signs. Since ##\frac {dB(t)}{dt} = - \beta##, we can write the corrected equation as $$\frac{Rm}{l} \ddot x + B(t)^2 l \dot x - \beta B(t) x = +\beta x_0 B(t_0)$$ Anyway, all of this leads to the need to make the sign correction for the second term on the left side of your Mathematica coded differential equation.

The signs are a nightmare. I also made a sign error in one of the terms of the differential equation. Now, I find that Mathematica no longer gives a manageable analytic solution using the command DSolve. However, I do get a numerical solution using NDSolve. So you can still plot ##v(t)##.

Note that with the sign corrections, your differential equation can be written as $$\ddot x + a(b-t)^2 \dot x - a(b-t)(x+x_0) = 0$$

Define a new x variable ##\tilde x= x + x_0##. ##\tilde x## represents the distance of the rod from the resistor. The area of the flux is then ##A = l\tilde x##. So, the initial value of ##\tilde x## is ##x_0##. The differential equation may then be written as $$\ddot {\tilde x} + a(b-t)^2 \dot {\tilde x} - a(b-t)\tilde x = 0$$ with initial conditions ##\tilde x(0) = x_0## and ##\dot {\tilde x} = 0##. Of course, at this point you can just drop the tilde with the understanding that ##x## now represents the redefined ##x##.

 

[TSny]

Why? What will happen if the magnetic field goes through zero and starts increasing linearly with the same slope out of the page?

I think you're right. We could assume ##B(t) = B_0 - \beta t## holds even beyond the time at which ##B = 0##. I think the differential equation would still be valid. I don't have much intuition about the large ##t## nature of the solutions in this case. Hopefully, we would not get solutions of the ODE for which the position of the rod ends up to the left of the resistor.