Momentum and collision related problem

[Finn007]

25.0-kg dog is trapped on a rock in the middle of a narrow river. A 66.0-kg rescuer has assembled a swing with negligible mass that she will use to swing down and catch the trapped dog at the bottom of her swing, and then continue swinging to the other side of the river. The ledge that the rescuer swings from is 5.0 m above the rock, which is not high enough so the rescuer and dog together can reach the other side of the river, which is 3.0 m above the rock. However, the rescuer can use a ladder to increase the height from which she swings. What is the minimum height of the ladder the rescuer must use so both dog and rescuer make it to the other side of the river? Assume that friction and air resistance are negligible.

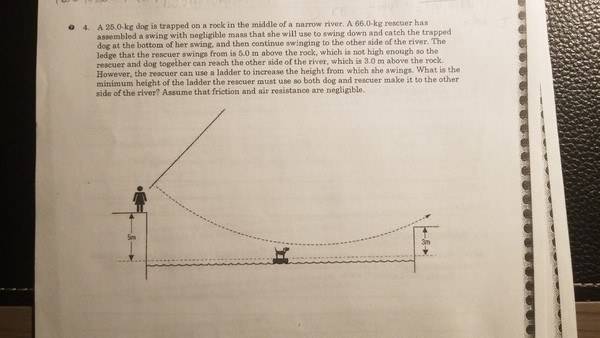
So far I've tried:

m_rg(h₁+h_l = (m_r+m_d)gh₂

but it seems to be giving a negative height for the ladder

 

[BvU]

Hello Finn,

Please use the template provided -- as described in the guidelines its use is mandatory

but it seems to be giving a negative height for the ladder

Oh, does it ? Show your work, please

 

[Finn007]

Hello Finn,

Please use the template provided -- as described in the guidelines its use is mandatory

Oh, does it ? Show your work, please

hl = (((mr+md)h2)/mr)-h1 = (((66+25)3)/66)-5 = -0.8636

 

[jbriggs444]

hl = (((mr+md)h2)/mr)-h1 = (((66+25)3)/66)-5 = -0.8636

Can you describe in words, what you are basing that equation on? It looks like a conservation of energy argument. But is energy conserved?

 

[BvU]

Well, if the outcome is somewhat unexpected, then perhaps there is something amiss in the assumptions ...
What were they ? (in other words: what is the assumption in the expression you used ?)

 

[Finn007]

Well, if the outcome is somewhat unexpected, then perhaps there is something amiss in the assumptions ...
What were they ? (in other words: what is the assumption in the expression you used ?)

Can you describe in words, what you are basing that equation on? It looks like a conservation of energy argument. But is energy conserved?

I think that energy is conserved based on my assumption but I'm not sure.

 

[jbriggs444]

I think that energy is conserved based on my assumption but I'm not sure.

Have you covered elastic and inelastic collisions in your coursework? If a rescuer collides with a dog and both move off together, which kind is it?

 

[Finn007]

Have you covered elastic and inelastic collisions in your coursework? If a rescuer collides with a dog and both move off together, which kind is it?

Inelastic? But I'm not sure which equations to use that could help me find the height. I was thinking m₁v_1i = (m₁+m₂)V

 

[jbriggs444]

Inelastic? But I'm not sure which equations to use that could help me find the height. I was thinking m₁v_1i = (m₁+m₂)V

It would be helpful if you could add some words instead of simply writing down an equation. It seems that you are using conservation of momentum for the event of the collision. That is a good move. If you know the rescuer's velocity prior to the event, you can use that equation to determine the rescuer+dog's velocity after.

[It is also helpful to define your variable names and what they mean. What is obvious to you may not be as obvious to your reader]

Now you just have to figure out v_1i (the velocity of the rescuer as he arrives at the dog). Perhaps a conservation of energy approach would work...

 

[Finn007]

It would be helpful if you could add some words instead of simply writing down an equation. It seems that you are using conservation of momentum for the event of the collision. That is a good move. If you know the rescuer's velocity prior to the event, you can use that equation to determine the rescuer+dog's velocity after.

[It is also helpful to define your variable names and what they mean. What is obvious to you may not be as obvious to your reader]

Now you just have to figure out v_1i (the velocity of the rescuer as he arrives at the dog). Perhaps a conservation of energy approach would work...

So how would I connect finding v_1i to the height? Should I use KE = mv²/2 and GPE = mgh?

 

[jbriggs444]

So how would I connect finding v_1i to the height? Should I use KE = mv²/2 and GPE = mgh?

Yes, that is what I would do.

 

[Finn007]

Yes, that is what I would do.

Yes, that is what I would do.

Can I assume that mv²/2 = mgh and v is v_1i?

 

[jbriggs444]

Can I assume that mv²/2 = mgh?

At the risk of repeating myself: use your words. For example...

You are invoking conservation of energy. No mechanical energy is lost as the rescuer swings from his starting perch to the position of the dog. We can justify that because the tension of the rope is at right angles to his path (no motion in direction of force means no work is done by the force) and because we assume that air resistance is negligible.

That means that ending mechanical energy is equal to starting mechanical energy.

The starting mechanical energy consists of kinetic energy and gravitational potential energy. We can write down an equation for that in terms of the initial velocity ##v_i## and the initial height ##h_i##

$$E_{i}=\frac{1}{2}mv_i^2 + mgh_i$$

The ending mechanical energy consists of kinetic energy and gravitational potential energy. We can write down an equation for that in terms of the final velocity ##v_f## and the final height ##h_f##.

$$E_{f}=\frac{1}{2}mv_f^2 + mgh_f$$

But we already know that ##E_i=E_f## so we can equate the two and rearrange terms:

$$\frac{1}{2}mv_f^2 + mgh_f = \frac{1}{2}mv_i^2 + mgh_i$$
$$\frac{1}{2}mv_f^2 - \frac{1}{2}mv_i^2 = mg(h_i-h_f)$$

But the initial velocity is zero. And we can choose coordinates where the final height is 0. If we then call the initial height "h", and the final velocity "v", this becomes:

$$\frac{1}{2}mv^2 = mgh$$

So you do not need to assume that mv²/2 = mgh. You can demonstrate it for the situation at hand.

 

[Finn007]

At the risk of repeating myself: use your words. For example...

You are invoking conservation of energy. No mechanical energy is lost as the rescuer swings from his starting perch to the position of the dog. We can justify that because the tension of the rope is at right angles to his path (no motion in direction of force means no work is done by the force) and because we assume that air resistance is negligible.

That means that ending mechanical energy is equal to starting mechanical energy.

The starting mechanical energy consists of kinetic energy and gravitational potential energy. We can write down an equation for that in terms of the initial velocity ##v_i## and the initial height ##h_i##

$$E_{i}=mv_i^2 + mgh_i$$

The ending mechanical energy consists of kinetic energy and gravitational potential energy. We can write down an equation for that in terms of the final velocity ##v_f## and the final height ##h_f##.

$$E_{f}=mv_f^2 + mgh_f$$

But we already know that ##E_i=E_f## so we can equate the two and rearrange terms:

$$mv_f^2 + mgh_f = mv_i^2 + mgh_i$$
$$mv_f^2 - mv_i^2 = mg(h_i-h_f)$$

But the initial velocity is zero. And we can choose coordinates where the final height is 0. If we then call the initial height "h", and the final velocity "v", this becomes:

$$mv^2 = mgh$$

So you do not need to assume that mv² = mgh. You can demonstrate it for the situation at hand.

Ohhh, okay.

So I'm doing first:
v_f2 = sqrt(2gh) = sqrt(2(9.8)(3)) = 7.7
for finding the velocity when they land at the other side.

Then use V = 7.7:
v_1i = ((m₁+m₂)V)/m₁ = ((66+25)/7.7)/66 = 10.6
for finding the velocity just before the rescuer reaches the dog.

Then use v = 10.6
h = v²/2g = (10.6)²/2(9.8) = 5.7

So the ladder height should be 5.7 - 5 = 0.7?

 

[jbriggs444]

So I'm doing first:
v_f2 = sqrt(2gh) = sqrt(2(9.8)(3)) = 7.7
for finding the velocity when they land at the other side.

So you are working backward. You know they land together on a 3 meter high platform with zero velocity. So they must have swung upward with a starting velocity of 7.7 meters per second^2 just after the pick-up.

[You are working with numbers. It is usually better to stick with algebra and variable names until the very end and plug in numbers as a final step. It makes errors in the algebra easier to spot and helps you see where things cancel. In particular, I believe you will find that g cancels out. The two places where you multiplied or divided by 9.8 were wasted arithmetic]

Then use V = 7.7:
v_1i = ((m₁+m₂)V)/m₁ = ((66+25)/7.7)/66 = 10.6
for finding the velocity just before the rescuer reaches the dog.

That looks good as well.

Then use v = 10.6
h = v²/2g = (10.6)²/2(9.8) = 5.7

So the ladder height should be 5.7 - 5 = 0.7?

Yes. Without carefully checking the arithmetic, it all looks correct.

 

[haruspex]

I believe you have found the intended answer, but

v_1i = ((m₁+m₂)V)/m₁ = ((66+25)/7.7)/66 = 10.6
for finding the velocity just before the rescuer reaches the dog.

That's a collision speed of 38kph. Perhaps not the wisest of rescue attempts.

 

[neilparker62]

Alternate method:

Energy loss during "collide and coalesce" collision given by $$ ½μΔv^2 $$ where $$ μ = \frac{m_1m_2}{m_1+m_2} $$ and Δv is the relative velocity between the colliding objects - in this case equal to ## \sqrt{2gh_1} ##. Thus $$ m_1gh_1-½ \frac{m_1m_2}{m_1+m_2}\times 2gh_1=(m_1+m_2)gh_2 $$. From which ## h_1 ## can be determined.