Minimization using Lagrange multipliers

[TheCanadian]

Given the following expressions:

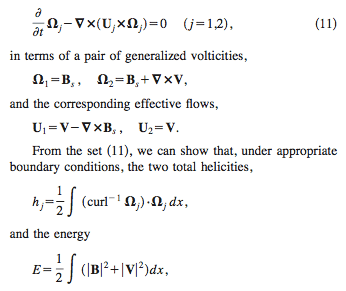
and that ## \bf{B}_s = \nabla \times \bf{A}_s ##

how does one solve for the following expressions given in (12) and (13)?

I've attempted doing so and derive the following expressions (where the hat indicates a unit vector):

## bV = \bf{ \hat{V}} \cdot {\bf{B}_s} + \bf{A}_s \cdot (\nabla \times \bf{\hat{V}}) ##

## {\bf{B}}_s \cdot (\nabla \times {\bf{\hat{A}}_s)} = B_s = ( \frac{1}{a} + \frac {1}{b}){B}_s + \frac{1}{2b}[\bf{V} \cdot (\nabla \times\bf{ \hat {A}}_s) + \bf{\hat {A}}_s \cdot (\nabla \times {\bf{V}})] ##

Although similar in some terms, this is clearly not equivalent to what's stated above after considering further vector identities and there is no curl(B) term present anywhere. It seems so simple yet my calculation is quite a bit off. If anyone could guide me through this with steps they've taken (and possibly ensure the above equations are actually correct), that would be kindly appreciated.

 

[dRic2]

You have an integral of the type
$$E = \int d^3x L(\phi(x), \partial_i \phi(x))$$
which should be minimized. First, I suggest you to re-write the function ##L## inside the integral in tensor notations, for example ##\mathbf B = ∇ \times \mathbf A## is written as ##B_a = \epsilon_{abc}\partial_{b} A_c## (with ##\partial_i## I mean ##\frac {\partial}{\partial x_i}##). Once you have done that, use Euler-Langrange equations for fields https://en.wikipedia.org/wiki/Lagrangian_(field_theory) and Eq. (12) and (13) should follow. I didn't do it, but it seems to me it should work.