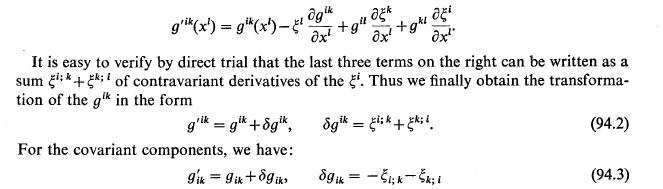- #1
Tursinbay
- 5
- 0
In the second volume, Field Theory, of popular series of Theoretical Physics by Landau-Lifschitz are given following equations as in attached file from the book. Here is considered metric change under coordinate transformation. How is the new, prime metric expressed in original coordinates is obtained as in (94.2). In right hand side of the equation right before (94.2) the last three terms is equal to Killing equations as it is said that could be verified by direct trial. What would direct trial like. I checked but got different results.