Maximum load capacity of a time dependant Force on the surface of a metal

[bravopipo]

Hello;
What equations on mechanics can I use or study in order to measure the maximum force in Newtons the surface of the metal Steel box can hold.

Details:
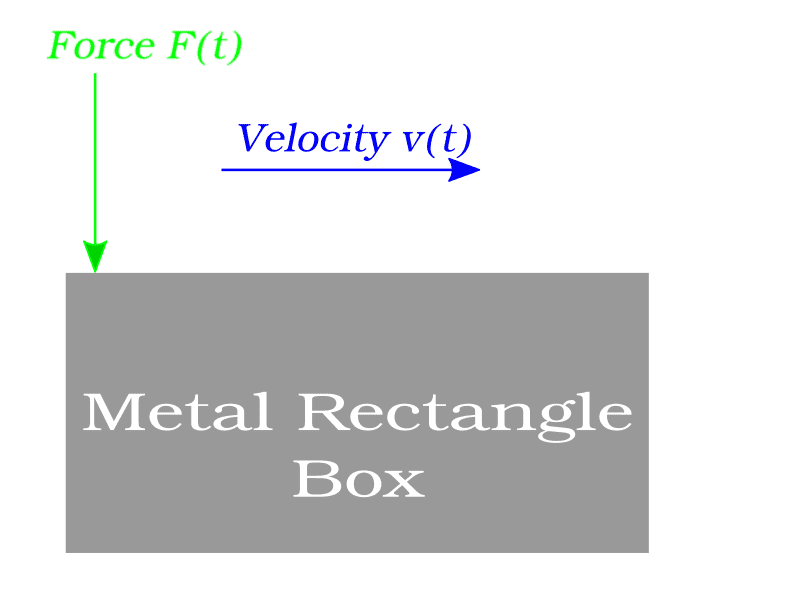
Watch the image below, we have a metal box made of let's say steel, this box have a shape of rectangle of a thickness of for example 1cm.
O the top face of the Box, we apply a force F(t) vertical to the surface of that top face, this force is not applied on a single point but a straight line of length let's say 1cm. The force F(t) vary with time and move at a speed v(t)=20m/s. The Force F(t) have also a frequency of 10Hz, this means that each straight line in the top face of the Box will receive the same amount of load F(t) after each 0.1 Seconds.

Question:
Because the force F(t) is not static, what equations can be used to estimate the maximum load the face of the box can tolerate without damage.
Is there any software that can resolve such problems without too much complexity ?

Regards

 

[Cutter Ketch]

I see that you recognize that this is a complex problem. Problems like these are usually addressed numerically by a process called finite element analysis using software such as ANSYS. Unfortunately ANSYS is expensive professional engineering software and probably beyond the scope of your problem. Perhaps you have a friend who is a professional mechanical engineer?

Failing that, you will probably want to make some significant simplifications, make an estimate, and then back off on the force to leave plenty of margin below the estimate. For example you could calculate the worst static case which should be when the force is maximum and located in the middle of the top surface of the box. What you want to calculate is the stress and keep it below the yield strength of the material. Unfortunately even that single static calculation is tough because it isn’t just the force per unit area under the probe. That force gets transferred through the steel. This bit pushes on that bit and that bit pulls on another bit creating a stress field throughout the material. For example, when you push in the middle, the material flexes like a trampoline and most of the top surface winds up in tension. In fact, the yield strength in tension will usually be the limiting factor. However, some places will be in compression, some places will experience shear, and a material will have different strengths for these different kinds of stress.

Depending how ambitious you are, it isn’t all that hard to make a finite element model in your favorite programming language. You can probably even find some free routines out there.

 

[Baluncore]

I do not believe the oscillation is important unless it continues for many hours. That is the subject of metal fatigue. https://en.wikipedia.org/wiki/Fatigue_(material)

The force must be applied to an area, NOT to a point or a line, or the surface pressure will punch a hypothetical hole through the hypothetical steel plate.

 

[bravopipo]

... What you want to calculate is the stress and keep it below the yield strength of the material. ... In fact, the yield strength in tension will usually be the limiting factor.

I already know that when doing static stress analysis, the material will receive a plastic deformation if the stress (for example von mises) go bigger than the material yield strength. But take a simple example, let's take a steel ball of mass 1Kg and drop it from an altitude of 1 Meter, the magnitude of the force of impact with a solid surface will be high for example 100 KN (Kilo Newtons), but the ball will still keep its shape untouched. Now try to make a static analysis to this ball with a force magnitude of 100 KN, and you see that the Stress in the ball Go Higher than its Yield Strength and the deformation is permanent!

What I want to do, is to know if the material will deform or no based on the amount of energy it receive and not the amount of force. I you apply a 100KN to steel ball for a duration of 0.01 seconds it won't deform like if you apply the same force magnitude of 100KN to the same ball during 1 seconds. Because the energy that the ball receive during 1 seconds is 100 Times higher than in 0.01 seconds.

In resume an energy study will be from my point of view much efficient for determining the resistance of a material to deformation rather than simply calculate stress of the force and compare it to the yield strength of the material. And that is what i am searching for, i still didn't find a document or thesis talks about it.

The force must be applied to an area, NOT to a point or a line, or the surface pressure will punch a hypothetical hole through the hypothetical steel plate.

Take a look at the image below, a steel cylinder that roll on the top face of the steel box. The contact between this cylinder and the surface face of the box is clearly a straight line, just tell me how can you make this type of contact on a surface and not a straight line ?! This kind of contact is omnipresent in mechanical components for example needle rollers.

 

[Cutter Ketch]

I already know that when doing static stress analysis, the material will receive a plastic deformation if the stress (for example von mises) go bigger than the material yield strength. But take a simple example, let's take a steel ball of mass 1Kg and drop it from an altitude of 1 Meter, the magnitude of the force of impact with a solid surface will be high for example 100 KN (Kilo Newtons), but the ball will still keep its shape untouched. Now try to make a static analysis to this ball with a force magnitude of 100 KN, and you see that the Stress in the ball Go Higher than its Yield Strength and the deformation is permanent!

What I want to do, is to know if the material will deform or no based on the amount of energy it receive and not the amount of force. I you apply a 100KN to steel ball for a duration of 0.01 seconds it won't deform like if you apply the same force magnitude of 100KN to the same ball during 1 seconds. Because the energy that the ball receive during 1 seconds is 100 Times higher than in 0.01 seconds.

In resume an energy study will be from my point of view much efficient for determining the resistance of a material to deformation rather than simply calculate stress of the force and compare it to the yield strength of the material. And that is what i am searching for, i still didn't find a document or thesis talks about it.Take a look at the image below, a steel cylinder that roll on the top face of the steel box. The contact between this cylinder and the surface face of the box is clearly a straight line, just tell me how can you make this type of contact on a surface and not a straight line ?! This kind of contact is omnipresent in mechanical components for example needle rollers.
View attachment 255257

Regarding the line of contact, I think you probably already understand the point being made and you don’t really mean an infinitely thin line of contact. I suspect you are using the word “line” in the casual sense rather than the mathematically precise sense. Just to be explicit so we can all agree, an infinitely thin line will exert an infinite pressure. The materials will deform increasing the contact patch until the net pressure balances against the stress resulting in a “fat line” area of contact.

Regarding the steel ball example, I get what you are saying, and I agree dynamics for finite time are not the same as statics. However, how big of an error that is depends on time scale. I don’t know your frequency. Seeing as you don’t have the best tool for the job you may have to back up to a problem you can do and try to reason to what degree it is a meaningful approximation.

By the way, a less computationally efficient but more easily understandable computational approach is the method of finite differences. It calculates much more slowly, but since it steps in time it is explicitly useful for dynamic problems.

 

[jrmichler]

The contact between this cylinder and the surface face of the box is clearly a straight line

No. The contact between a "long" cylinder and a flat surface is a rectangle. Search Hertzian contact stress for more information. The case of a cylinder against a flat plate is the same as two parallel cylinders where one cylinder has infinite radius.

Similarly, a sphere hitting a surface has a force vs deformation that can be calculated using the Hertzian contact stress theory. If you integrate the force vs deflection until it equals the initial kinetic energy of the ball, you can calculate the peak force, peak deflection, and peak stress.

The contact stress at yield will be higher than the published yield strength of the material. The published yield strength is based on compressing a cylindrical specimen that is free to squish yield sideways. In a contact stress situation, the compressed area is surrounded by material that prevents it from yielding. The simplified case below shows a compressive force over a finite area in a seminfinite plate. The yield stress in this case is three times the published yield stress for a cylindrical specimen. Contact stress is similar.

 

[Baluncore]

This kind of contact is omnipresent in mechanical components for example needle rollers.

A reciprocating roller needs a larger diameter to conform to the flexed sheet without causing damage. Brinelling of the surface can be expected. It will need to be lubricated or dissimilar materials.

But the limiting situation will be where the roller approaches or contacts the boundary of the plate supported by the box boundary wall, where the surface will not be deflected.

We have not been told what situation is actually being modeled. Is this a frictional or a rolling contact?

 

[bravopipo]

Okay, let's do some practical example, we have a cube made of steel, the cube side equal 10mm and have a fillet on the top right edge. The fillet radius is 2mm.
The steel used have the following mechanical characteristics:
Elastic Modulus : 215000 N/mm2 (215000 MPa)
Poison ratio : 0.28
Yield Strength : 785 MPa
Shear Modulus : 79000 MPa

The top right edge is exposed to an horizontal force of magnitude 15KN (15 Kilo Newtons). The botton side of the cube is fixed. The results below are for non linear static analysis.

The stress analysis clearly show that:
1. The maximum stress exceed the Yield Strength of the material but in a very small and tiny spot, otherwise the entire rest of cube is within limits.
2. Maximum deflection is 0.066 mm
3. Maximum energy is : 0.001933 N.m = 0.001933 Joule

Suppose that we want to periodically apply this force with the same magnitude for a duration of 0.1 seconds each 1 second. Can the edge of the cube withstand this type of loading and for how many times before failure, (1000 cycles, 1 million cycles, 1 billion cycles) ?

Stress Analysis :

Displacement Analysis :

Strain Analysis : (Energy N.m)

 

[Baluncore]

1. The maximum stress exceed the Yield Strength of the material but in a very small and tiny spot, otherwise the entire rest of cube is within limits.

During the first application of force, yield will permanently deform and broaden the contact area. The second identical force application will not yield, but will remain elastic over the previously deformed area.

The question arises, is it the same item that applies the force every time? Does it strike in exactly the same place, or is it sufficiently different or sharp that it will yield every time?

This may best be analysed as a cold forging or a peening process.

 

[Cutter Ketch]

In your example the force is applied at a mathematical point. The stress is infinite. The only reason it isn’t infinite is that the model has finite sized elements in the mesh. In any real system the edge will deform elastically increasing the contact area with whatever is doing the pushing until either the stress is within the elastic limit or the steel deforms. To do this kind of thing more correctly put the box and some structure it is pushing against in the model. You will see the stress deforms both objects and the contact patch grows. You will find that the maximum local stress is actually much lower than this calculation shows and may well be within the elastic limit for both objects.

 

[bravopipo]

The question arises, is it the same item that applies the force every time? Does it strike in exactly the same place, or is it sufficiently different or sharp that it will yield every time?

The force start from let's say the middle of the right side, move upward and passes the fillet then it stop at the end of the fillet. The item that apply this force move at a velocity of 10m/s and the magnitude of the force is considered the same so always 15KN. This entire process have a frequency of 10 Hz.

If I understand, you mean that once the first deformation happen due to the first applied force of 15KN, the next times the same magnitude in applied will not cause further Yield. If so then it is fine.

 

[Baluncore]

If I understand, you mean that once the first deformation happen due to the first applied force of 15KN, the next times the same magnitude in applied will not cause further Yield. If so then it is fine.

It is reasonable to use “plastic design” to create an object that will relieve inbuilt stress by plastic deformation in the environment. Deliberately reducing the wall thickness can make it more durable.

But the 10 Hz is still going to require fatigue analysis. There may be problems if the box is resonant at a multiple of 10 Hz. Is there material in the box that would dissipate vibrational energy?

 

[bravopipo]

I don't know about vibration energy, I will make research on that to see how to dissipate it