- #1
MLars
- 2
- 0
Hello Physics Forums!
I am currently writing a computer program that displays an enthalpy-pressure diagram for the refrigerant 134a. I am using the data and relation between specific volume, pressure and temperature found in http://eng.sut.ac.th/me/2014/document/LabMechanical1/HFC-134a_SI.pdf. My algorithm is able to calculate the correct volume given a pressure and temperature, however the total enthalpy calculation differs from the diagram found in the above paper.
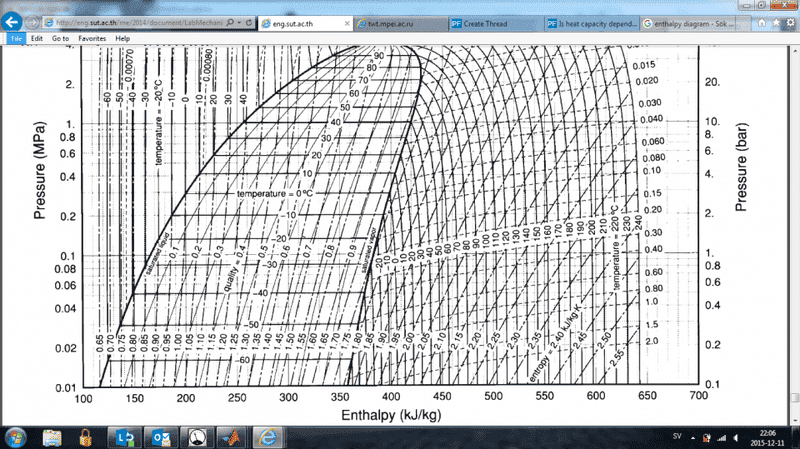
In particular, in the liquid state, my temperature curves are not that vertical but fall to the right as pressure increases. According to my understanding of specific enthalpy it is defined as h=u+pv where u is a function of only temperature. Now to my question. If the above is true, how can the lines in the diagram be almost vertical when the specific volume is close to constant and the pressure increases by a factor of 10(pv should increase x10). May u be dependent on pressure, compensate for the increasing pv and yield a constant enthalpy? What am I missing?
Thanks a lot
Mike
I am currently writing a computer program that displays an enthalpy-pressure diagram for the refrigerant 134a. I am using the data and relation between specific volume, pressure and temperature found in http://eng.sut.ac.th/me/2014/document/LabMechanical1/HFC-134a_SI.pdf. My algorithm is able to calculate the correct volume given a pressure and temperature, however the total enthalpy calculation differs from the diagram found in the above paper.
In particular, in the liquid state, my temperature curves are not that vertical but fall to the right as pressure increases. According to my understanding of specific enthalpy it is defined as h=u+pv where u is a function of only temperature. Now to my question. If the above is true, how can the lines in the diagram be almost vertical when the specific volume is close to constant and the pressure increases by a factor of 10(pv should increase x10). May u be dependent on pressure, compensate for the increasing pv and yield a constant enthalpy? What am I missing?
Thanks a lot
Mike