Identity involving exponential of operators

[thatboi]

Hey all,
I saw a formula in this paper: (https://arxiv.org/pdf/physics/0011069.pdf), specifically equation (22):

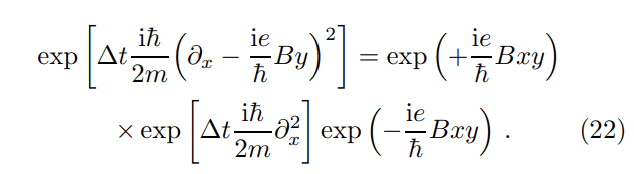
and wanted to know if anyone knew how to derive it. It doesn't seem like a simple application of BCH to me.
Thanks.

 

[vanhees71]

Please use LaTeX to type formulae. It's much easier to read!

The trick is that
$$(\partial_x - \mathrm{i} e/\hbar By)\psi (\vec{x}) = \exp(\mathrm{i} e B x y/\hbar) \partial_x \left [\exp(-\mathrm{i} e B x y/\hbar) \psi(\vec{x}) \right]$$
for all ##\psi(\vec{x})## (in the domain of the operators applied ;-)).

By iteration it's further easy to see that for ##k \in \mathbb{N}##
$$(\partial_x - \mathrm{i} e/\hbar By)^k\psi (\vec{x}) = \exp(\mathrm{i} e B x y/\hbar) \partial_x^k \left [\exp(-\mathrm{i} e B x y/\hbar) \psi(\vec{x}) \right].$$
Plugging this into the series defining the operator exponential you get Eq. (22) of the paper.

 

[topsquark]

Or, leaving out a lot of details: ##[\partial _x, y] = 0##.

-Dan