- #1
jwxie
- 281
- 0
Hi.
Let A = 1,2,3,4,5,6,7
How many symmetric relations on A contain exactly (a) four ordered pairs, (b) 5 , (c) seven and (d) eight
The book has solutions to the first two, which I didn't understand at all.
Please look the pic below
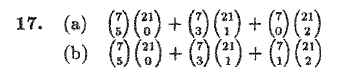
Can someone guide me through how to approach the problem?
Thanks
Let A = 1,2,3,4,5,6,7
How many symmetric relations on A contain exactly (a) four ordered pairs, (b) 5 , (c) seven and (d) eight
The book has solutions to the first two, which I didn't understand at all.
Please look the pic below
Can someone guide me through how to approach the problem?
Thanks