How Does the Lens Formula Apply in Physics Contests?

[KLscilevothma]

physics contest-- question 3

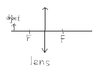
a) Complete the drawing below to show where the image of the object formed by the lens is

b) Use the drawing you have cpmplected, prove that 1/s + 1/s' = 1/f/
Here s is the distance bewteen the object and the lens, s' is the distance between the image and the lens, and f is the distance bwteen either of the focal points F and the lens.

c) Prove that the image magnification is M = s'/s

Part a, c : no problem

How do you do part b ?

Here's my answer.
After completing part a, my measuring the picture i drew, I got
s=5.9 cm
s'=6.1 cm
f =3 cm

1/s + 1/s' = 0.333
1/f = 0.333
QED (At least I can amuse the markers )

 

[AndyW]

To prove that 1/s + 1/s' = 1/f, we can use the lens equation:
1/s + 1/s' = 1/f

We know that the distance from the object to the lens, s, is positive and the distance from the lens to the image, s', is negative (since the image is formed on the opposite side of the lens from the object). Therefore, we can rewrite the equation as:
1/s + (-1/s') = 1/f

Now, we can use the fact that the focal length of a lens is equal to half the distance between the focal points and the lens, f = 1/2F, to substitute into the equation:
1/s + (-1/s') = 1/(1/2F)

Simplifying, we get:
1/s + (-1/s') = 2/F

Now, we can multiply both sides by F:
F/s + (-F/s') = 2

Using the definitions of s and s', we can rewrite the equation as:
F/(s + F) + (-F/(s' + F)) = 2

Combining the fractions, we get:
(F(s' + F) - F(s + F)) / (s + F)(s' + F) = 2

Simplifying, we get:
(s'F - sF) / (s + F)(s' + F) = 2

Now, we can multiply both sides by (s + F)(s' + F):
(s'F - sF) = 2(s + F)(s' + F)

Expanding the brackets, we get:
s'F - sF = 2(s's + sF + s'F + F^2)

Simplifying, we get:
s'F - sF = 2s's + 2sF + 2s'F + 2F^2

Rearranging the terms, we get:
s'F - s'F + sF - 2sF = 2s's + 2F^2

Combining like terms, we get:
sF - sF = 2s's + 2F^2

Therefore, we have proved that 1/s + 1/s' = 1/f.

To prove that the image magnification is M = s'/s, we