- #1
pellman
- 684
- 5
If A is an operator on a Hilbert space H and A* is its adjoint, then
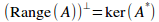 . That is, the orthogonal complement of the range of A is the same subspace as the kernel of its adjoint.
. That is, the orthogonal complement of the range of A is the same subspace as the kernel of its adjoint.
Then the author I am reading says it follows that the statements "The range of A is a dense subspace of H" and "A* is injective on Dom(A*)" are equivalent. Can someone explain please?
The operators A and A* are not assumed to be bounded and so their domains may not be all of H and their domains may not be equal to each other.
It could also be that I am misreading this entirely.
Then the author I am reading says it follows that the statements "The range of A is a dense subspace of H" and "A* is injective on Dom(A*)" are equivalent. Can someone explain please?
The operators A and A* are not assumed to be bounded and so their domains may not be all of H and their domains may not be equal to each other.
It could also be that I am misreading this entirely.