- #1
CMATT
- 32
- 1
A suspension bridge oscillates with an effective force constant of
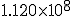 N/m.
N/m.
(a) How much energy is needed to make it oscillate with an amplitude of 0.106 m?
(b) If soldiers march across the bridge with a cadence equal to the bridge's natural frequency and impart
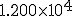 J of energy each second, how many minutes does it take for the bridge's oscillations to go from 0.106 m to 0.530 m amplitude, assuming the bridge has no damping?
J of energy each second, how many minutes does it take for the bridge's oscillations to go from 0.106 m to 0.530 m amplitude, assuming the bridge has no damping?
RELEVANT EQUATIONS:
For (a)
Etot = (.05)(k)(xmax)^2
For (b)
not sure
THE ATTEMPT AT THE SOLUTION:
a)
k = 1.120E8 N/m
xmax^2 = .106 m
Etot = (.05)(k)(xmax)^2 = (.05)(1.120E8)(.106) = 6.29E5 J
This answer was correct on my webassign
b) I'm very confused here. All I know is 6.29E5 J is the energy required to make it oscillate with an amplitude of .106 m
(a) How much energy is needed to make it oscillate with an amplitude of 0.106 m?
(b) If soldiers march across the bridge with a cadence equal to the bridge's natural frequency and impart
RELEVANT EQUATIONS:
For (a)
Etot = (.05)(k)(xmax)^2
For (b)
not sure
THE ATTEMPT AT THE SOLUTION:
a)
k = 1.120E8 N/m
xmax^2 = .106 m
Etot = (.05)(k)(xmax)^2 = (.05)(1.120E8)(.106) = 6.29E5 J
This answer was correct on my webassign
b) I'm very confused here. All I know is 6.29E5 J is the energy required to make it oscillate with an amplitude of .106 m
Last edited by a moderator: