How Do You Model a Torsion Spring in a Pendulum's Lagrangian?

[Amat3r]

Hello!

I'd like to ask for help with one problem :) thank you in advance.

1. Write the equations for kinetic and potential energy for the pendulum with rectangular prism of size a*b*c (width, length, depth). With the Lagrange's equation get the equation of motion. The block is homogeneous with mass m. We also have a torsion spring with coefficient k. J is a moment of inertia. Angle is q (or phi if you prefer).

So it is a theoretical task. The bold characters are supposed to be known as seen on the sketch.

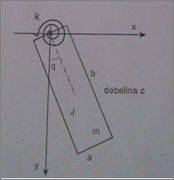
2. Am I right with this?

Wp (potencial energy) = m * g * b/2 * (cos(q) - 1)

Wk (kinetic energy) = 1/2 * J * ω^2

ω = dot(q)

J = 1/12 * m * (a^2 + b^2) + m * (b/2)^2

Where do I include the spring?

 

[Asim Riaz]

The equation of motion with Lagrange's equation is: m*ddot(q) + m*g*b/2*sin(q) = k*b/2*(cos(q) - 1)You need to include the spring in the equation of motion, which you have done. The term k*b/2*(cos(q) - 1) accounts for the tension in the spring, where k is the spring coefficient and b is the length of the prism.