How Do You Integrate Work with a Changing Angle Theta?

[morssolis]

here is the problem. w= f*d*cos(theta). theta is changing so it involves integration.

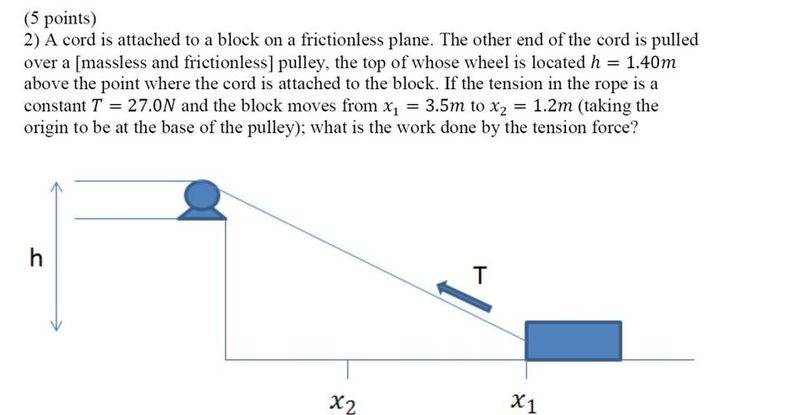
i know the answer its about 52. i know one solution for it but i have been trying to figure out how to solve it integrating with respect to theta. the way i know to solve it is let

cos(theta)= x / ((x^2)+(h^2))^(-1/2), then integrate this with respect to x with a u substitution.



i thought that the integral from theta at x1 to theta at x2 of F*d*cos(x) dtheta would work, however it does not. i have been trying to figure this out for days.

any ideas how you can solve this by integrating with theta as opposed to x?

Thanks

 

[ehild]

[tex]W=\int_{x1}^{x2}{F \cos{\theta} dx}[/tex]

It is easy to integrate by substituting u=x^2+h^2.

ehild

 

[morssolis]

well thank you for the input however i know that already. i said that in the OP. i am trying to figure out how to integrate with respect to theta

 

[ehild]

F=T is constant. Substitute x / ((x^2)+(h^2))^(-1/2) for cos(theta) in the integral and calculate it.

ehild

 

[rwisz]

for sharing your problem and solution with us. It seems like you have a good understanding of the concept and have already tried different approaches to solve it.

Integrating with respect to theta instead of x can be a bit tricky, but it is definitely possible. One way to approach this problem is to use the substitution method, where you substitute x = h*tan(theta) and then use the trigonometric identity cos^2(theta) = 1/(1+tan^2(theta)) to simplify the expression. This will result in an integral that is easier to solve with respect to theta.

Another approach could be to use the chain rule in reverse, where you differentiate the expression with respect to theta and then integrate it. This can be useful if the expression is not in a form that can be easily integrated using substitution.

I would also suggest breaking down the integral into smaller parts and solving them separately. This can help in simplifying the overall expression and making it easier to integrate.

Overall, solving problems involving non-constant theta can be challenging, but with persistence and different approaches, you will eventually find a solution. Best of luck!