- #1
mathmari
Gold Member
MHB
- 5,049
- 7
Hey! 
I am looking at the following:
The average tallest men live in Netherlands and Montenegro mit $1.83$m=$183$cm.
The average shortest men live in Indonesia mit $1.58$m=$158$cm.
The standard deviation of the height in Netherlands/Montenegro is $9.7$cm and in Indonesia it is $7.8$cm.
The height of a giant of Indonesia is exactly 2 standard deviations over the average height of an Indonesian. He goes to Netherlands. Which is the part of the Netherlands that are taller than that giant?
I thought to do the following:
Since the height of a giant of Indonesia is exactly 2 standard deviations over the average height of an Indonesian, we get that his height is $158+2\cdot 7.8=173.6$cm, right?
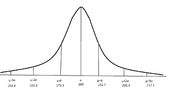
We have the following:
View attachment 6314
Now we want to compute $P(x>173.6)=1-P(x\leq 173.6)$, right? (Wondering)
At the graph we have $173.3$ how could we compute the $P(x\leq 173.6)$ ? (Wondering)
I am looking at the following:
The average tallest men live in Netherlands and Montenegro mit $1.83$m=$183$cm.
The average shortest men live in Indonesia mit $1.58$m=$158$cm.
The standard deviation of the height in Netherlands/Montenegro is $9.7$cm and in Indonesia it is $7.8$cm.
The height of a giant of Indonesia is exactly 2 standard deviations over the average height of an Indonesian. He goes to Netherlands. Which is the part of the Netherlands that are taller than that giant?
I thought to do the following:
Since the height of a giant of Indonesia is exactly 2 standard deviations over the average height of an Indonesian, we get that his height is $158+2\cdot 7.8=173.6$cm, right?
We have the following:
View attachment 6314
Now we want to compute $P(x>173.6)=1-P(x\leq 173.6)$, right? (Wondering)
At the graph we have $173.3$ how could we compute the $P(x\leq 173.6)$ ? (Wondering)