- #1
AngelofMusic
- 58
- 0
This is a question about finding the resultant of the force system.
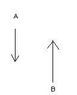
Basically, there is a rigid body with 3 pairs of forces with the same magnitude that are parallel to each other and in opposite directions. (I've attached an example of one of those pairs.) All three pairs are attached at different places on a long beam.
I converted one of the forces in each pair into a force-couple system. That means that each pair now has the forces cancelling each other out, and an additional moment (torque) vector.
(i.e. I moved the vector starting at A to point B, and found the torque of A once it has been moved to point B. Then the two forces cancel out.)
I was just wondering - do I also need to calculate the torque at point B when adding all the torques together? Since the torque is supposed to be a free vector, does that mean that all 3 of the resulting torques (with the pairs of forces in different places) can just be added together?
Also, since the forces are along the x and y axis, and the torques are perpendicular to that plane, would that make the resultant moment (torque) solely in the z-axis, then?
The textbook is incredibly confusing on this topic, and I'd appreciate any clarification!
Basically, there is a rigid body with 3 pairs of forces with the same magnitude that are parallel to each other and in opposite directions. (I've attached an example of one of those pairs.) All three pairs are attached at different places on a long beam.
I converted one of the forces in each pair into a force-couple system. That means that each pair now has the forces cancelling each other out, and an additional moment (torque) vector.
(i.e. I moved the vector starting at A to point B, and found the torque of A once it has been moved to point B. Then the two forces cancel out.)
I was just wondering - do I also need to calculate the torque at point B when adding all the torques together? Since the torque is supposed to be a free vector, does that mean that all 3 of the resulting torques (with the pairs of forces in different places) can just be added together?
Also, since the forces are along the x and y axis, and the torques are perpendicular to that plane, would that make the resultant moment (torque) solely in the z-axis, then?
The textbook is incredibly confusing on this topic, and I'd appreciate any clarification!