- #1
- 1,323
- 2
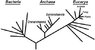
I have observed that many people have question about evolution. When I look back at high school we got to learn the classical model (see diagram below) of evolution and this model was also though in the university level zoology and plant biology whereas in microbiology we got to learn the Woese model of evolution based on 16/18 rRNA (the paper for the propose model is free on this site http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pubmed&pubmedid=2112744) rather than the classical model. Woese model of evolution (the attach picture show his proposed model) is more accurate than the classical model. Woese also proposed a model for cell evolution that goes with his evolution tree. Here a link for the paper and it's free http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pubmed&pubmedid=12077305
What I was wodering is how many people are aware of Woese model of evolution?
If you know Woese's model where did you learn about it.
If you never hear of Woese's model would you be interrested in learning more (maybe I'll write a paper).
Classical Model of Evolution (I simplified the model therefore it's not as accurate as desired)
Plant Animal Fungi
| | |
| | |
| | |
|__________|______________|
|
Protozoan
|
|
Bacteria
|
|
ArcheaBacteria
|
First single Cell
Additional link for Woese model
http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pubmed&pubmedid=10900003 (Interpreting the universal phylogenetic tree)
http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pubmed&pubmedid=11537862 (On the Nature of Global Classification)
What I was wodering is how many people are aware of Woese model of evolution?
If you know Woese's model where did you learn about it.
If you never hear of Woese's model would you be interrested in learning more (maybe I'll write a paper).
Classical Model of Evolution (I simplified the model therefore it's not as accurate as desired)
Plant Animal Fungi
| | |
| | |
| | |
|__________|______________|
|
Protozoan
|
|
Bacteria
|
|
ArcheaBacteria
|
First single Cell
Additional link for Woese model
http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pubmed&pubmedid=10900003 (Interpreting the universal phylogenetic tree)
http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pubmed&pubmedid=11537862 (On the Nature of Global Classification)
Attachments
Last edited by a moderator: