- #1
Kaushik
- 282
- 17
- Homework Statement
- Find the range of ##f(x) = 6^x + 3^x + 6^{-x} + 3^{-x} + 2##
- Relevant Equations
- AM >= GM
##f(x) = 6^x + 3^x + 6^{-x} + 3^{-x} + 2##
But, ## AM >= GM##
So,
##f(x) >= 5 * 2 ^ {\frac{1}{5}}##
But this is not the case. According to the graph, it is ## f(x) >= 6##.
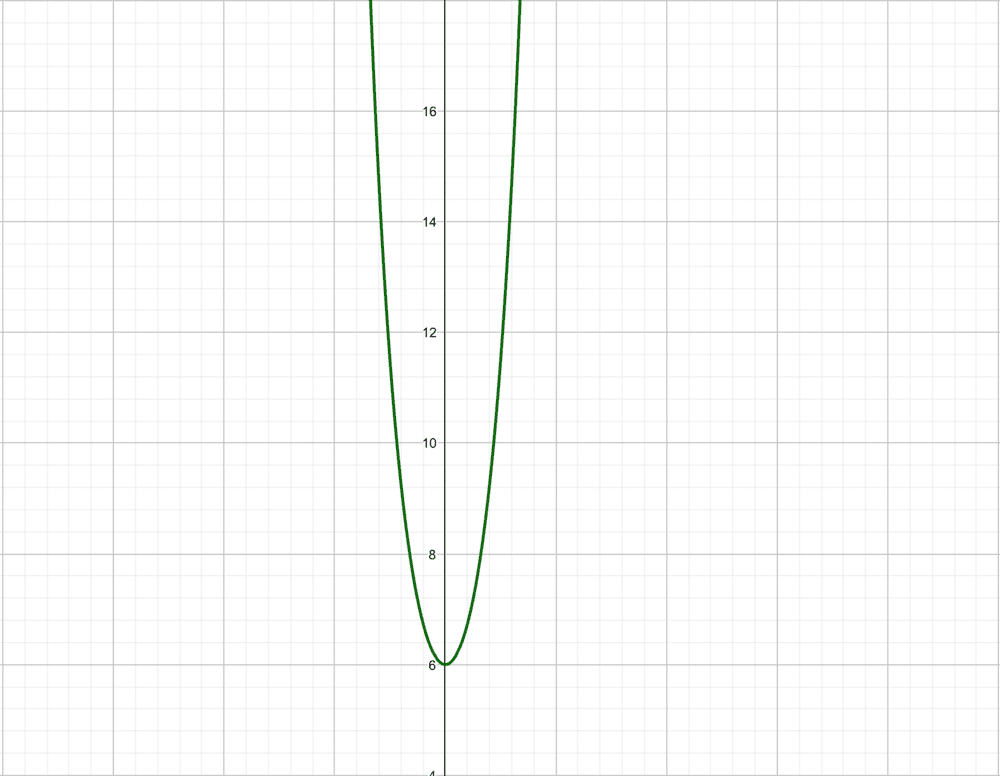
If I do the same thing without considering the constant '2' then I am getting the answer.
let ##g(x) = 6^x + 3^x + 6^{-x} + 3^{-x} ## and ##f(x) = g(x) + 2##
Using ##AM>=GM##,
##g(x) >= 4##
Hence, ##f(x) >= 6##
Why is this the case? Why is the latter approach working but no the former?
But, ## AM >= GM##
So,
##f(x) >= 5 * 2 ^ {\frac{1}{5}}##
But this is not the case. According to the graph, it is ## f(x) >= 6##.
If I do the same thing without considering the constant '2' then I am getting the answer.
let ##g(x) = 6^x + 3^x + 6^{-x} + 3^{-x} ## and ##f(x) = g(x) + 2##
Using ##AM>=GM##,
##g(x) >= 4##
Hence, ##f(x) >= 6##
Why is this the case? Why is the latter approach working but no the former?
